简单-中等题

概率论
哈希
- 169. 多数元素
双指针
- 26. 删除排序数组中的重复项
- 27. 移除元素
- 28. 实现 strStr()
- 38. 外观数列
- 58. 最后一个单词的长度
- 89. 合并两个有序数组
- 125. 验证回文串
- 141. 环形链表
- 167. 两数之和 ||
- 228. 汇总区间
查找及插入问题
- 二分查找及其变种
- - 33. 搜索旋转排序数组
  - 35. 搜索插入位置
  - 69. x的平方根
  - 153. 寻找旋转排序数组中的最小值
  - 704. 二分查找
  - 852. 山脉数组的峰顶索引
队列、栈
- 155. 最小栈
- 895. 最大概率栈（Hard）
- 单调栈
- - 42. 蓄水池
  - 84. 柱状图中的最大矩形
  - 496. 下一个更大元素|
  - 738. 每日温度
  - 901. 股票价格跨度
数组
- 66. 加一
- 67. 二进制求和
- 189. 旋转数组 middle
- 560. 和为k的子数组
- 674. 最长连续递增序列
链表
- 19. 删除链表的倒数第N个结点
- 83. 删除排序链表中的重复元素(hash)
- 138. 复制带随机指针的链表
- 141. 环形链表
- 160. 相交链表
- 203. 移除链表元素
树
- 100. 相同的树（递归）
- 101. 对称二叉树
- 104. 二叉树的最大深度
- 107. 二叉树的层序遍历 ||
- 108. 将有序数组转换为二叉搜索树（递归）
- 110. 平衡二叉树
- 111. 二叉树的最小深度
- 112. 路径总和
动态规划
- 53. 最大子序和
- 70. 爬楼梯
- 121. 买卖股票的最佳时机 |
- 122. 买卖股票的最佳时机 ||
- 198. 打家劫舍
- 343. 整数拆分（中等）
位运算
- 67. 二进制求和
- 137. 只出现一次的数字（1） middle
- 187. 重复的DNA序列 middle
- 191. 位1的个数
- 260. 只出现一次的数字（2） middle
- 318. 最大单词长度乘积 middle
- 421. 数组中两个数的最大异或值 middle
数学、矩阵
- 50. pow(x,n) middle
- 70. 爬楼梯
- 118. 杨辉三角 |
- 119. 杨辉三角 ||
- 168. Excel表列名称
- 171. Excel表列序号
- 172. 阶乘后的零
- 1232. 缀点成线
图论
- 遍历：深度优先遍历、广度优先遍历、并查集
- - 399. 除法求值 middle
  - 547. 省份数量
  - 684. 冗余连接 middle
  - 721. 账户合并
  - 947. 移除最多的同行或同列石头
  - 1202. 交换字符串的元素 middle
  - 1631. 最小体力消耗路径
- 最小生成树
- - 1584. 连接所有点的最小费用
连通域
- 200. 岛屿数量
- 595. 岛屿的最大面积

摸鱼摸了很久，这次重新刷题，会陆续补上中等题。早期的一些问题在单独博客里有细致的解释和资料参考。

概率论

一随机数以概率 p 生成0，以概率（1-p）生成1，怎样生成等概率的 0 和 1？
给定函数f(x)以概率p生成0，以概率(1-p)生成1，
那么可以得到g(x) = f(x)>0? 0:1，以概率p生成1，以概率(1-p)生成0；
当f(x) g(x)同时生成0的概率为p(1-p)，同时生成1的概率为p(1-p)；
因此实现了等概率地生成0和1.

哈希

169. 多数元素

方法：

暴力解法，枚举数组中的每个元素，再遍历一遍数组统计其出现次数，时间复杂度为 O(N^2) 的算法
哈希表法，使用hash表快速统计每个元素出现的次数，可以实现时间复杂度为O(n),但占用额外的空间，空间复杂度为O(n)
排序，对于数组中出现次数大于 ⌊ n/2 ⌋ 的元素，当数组长度为偶数时，则众数最小为n//2+1，当数组长度为奇数时，则众数最小为n//2+1；当对整个数组中元素按照升序或者降序排列，则第n//2+1个元素一定为众数，即下标为n//2的元素（下标从0开始）元素一定为众数
Boyer-Moore 投票算法

# Hash
class Solution:def majorityElement(self, nums: List[int]) -> int:hash = {}for i in nums:hash[i] = hash.get(i,0)+1return sorted(hash.items(), key = lambda kv:(kv[1], kv[0]))[-1][0]
# Sort
class Solution:def majorityElement(self, nums: List[int]) -> int:n = len(nums)nums.sort()return nums[n//2]
# Boyer-Moore投票
class Solution:def majorityElement(self, nums: List[int]) -> int:count = 0c = Nonefor i in nums:if count==0:c = icount += 1 if c==i else -1return c

双指针

双指针：

快慢指针
左右指针（二分查找是左右指针的一种）

26. 删除排序数组中的重复项

27. 移除元素

# 双指针法
# 方法一：直接快慢指针，对于快指针搜索不为val的元素，
# 依次前移填补满指针的位置，[4,1,2,3,5]，当val为4时，移动次数较多
class Solution:def removeElement(self, nums: List[int], val: int) -> int:temp = 0 length = len(nums)for i in range(length):if nums[i]!=val:nums[temp] = nums[i]temp = temp + 1return temp# 方法二：当需删除元素较少时当遇到val时，与队尾元素交换，
# 并减少元素数组长度，可以减少移动次数，并符合“元素顺序可以改变的要求”
class Solution:def removeElement(self, nums: List[int], val: int) -> int:temp = 0 length = len(nums)while(temp<length):if nums[temp]==val:nums[temp] = nums[length-1]length = length-1else:temp = temp + 1return temp

28. 实现 strStr()

主要方法有：

子串匹配：线性时间复杂度
双指针：线性时间复杂度
查找算法：BM、KMP、Sunday

对于方法1、方法2都有多余的操作，KMP则KMP 算法永不回退 txt 的指针 i，不走回头路（不会重复扫描 haystack），而是借助 dp 数组中储存的信息把 needle 移到正确的位置继续匹配，时间复杂度只需 O(N)，用空间换时间。KMP原理上类似于有穷状态转换机，主要操作包括，根据needle建立有穷状态转换机（用状态0-1-2-3-4表示needle中0、1、2、3、4对应的字符），根据有穷状态机在haystack中搜索。

# 双指针 从初始位置i开始，匹配haystack与needle，指针前移
# 如果匹配失败，haystack指针回到i+1，needle指针回到0
# 考虑needle为空字符串，返回0
class Solution:def strStr(self, haystack: str, needle: str) -> int:if needle=='':return 0n_index = 0  # needle指针 i = 0  # haystack指针h_length = len(haystack)n_length = len(needle)while(i < h_length):if haystack[i]==needle[n_index]:n_index = n_index + 1i = i + 1if n_index == n_length:return i-n_indexelse:i = i - n_index + 1  # 回溯的位置很关键n_index = 0return -1# mississippi
# issip
# i = 5  n_index = 4  i = 2

38. 外观数列

底子依旧是双指针问题，只需要写出在每个循环中求解问题的子函数，就可以通过循环调用子函数来解决问题。在子函数中使用双指针来取连续相同元素的数目。

双指针遍历有一个问题，当判断条件为相邻元素差异的时候，对序列x，需要比较x[i]与x[i+1]，首先x+1存在溢出风险，需要限定x+1<length，并且此时x只能取到x[length-2]，故此时抛弃了最后一个元素x[length-1]。
暂时的解法是在序列后加一个必然产生差异的元素，在遍历的过程中，正好抛弃掉最后一个额外元素，实现最终结果。（待学习）

取消for循环，用end遍历，依次加1，循环条件为while end<length，则可以将end和start取到最后一个位置。在这个题目中比较start和end的值进行比较，避免了跟边界值的比较。

总结：

当双指针遍历时，尽量避免使用for，而直接使用while，跟踪right指针来结束循环。
如果外循环为while，那么内循环大概率也需使用while循环，循环条件也要加上边界避免在内循环直接超出边界，同时尽量类比start而不是前一个元素或者后一个元素（此时会漏掉边界元素）。

class Solution:def countAndSay(self, n: int) -> str:index = '1'for i in range(n-1):index = self.turn(index)return indexdef turn(self, index_):index_ = index_+'#'start = 0ans = ''length = len(index_)for i in range(length-1):if index_[i]!=index_[i+1]:end = ians = ans+(str(end-start+1)+index_[i])start = i + 1return ans# 新子函数
def turn(self, index_):start = 0end = 0ans = ''length = len(index_)while end < length:while end<length and index_[start]==index_[end]:end = end+1ans = ans+(str(end-start)+index_[start])start = endreturn ans

58. 最后一个单词的长度

同38. 外观数列

# 求最后一个单词的长度，直接逆序双指针
# 先循环过滤掉' '，确定单词的终止位置
# 再循环单元字符，确定单词的开始位置，直接返回
# 如果正序双指针，需要移除字符串末尾的' '
class Solution:def lengthOfLastWord(self, s: str) -> int:n = len(s)start = n-1end = n-1while end>=0:while end>=0 and s[end]==' ':end = end-1start = endwhile end>=0 and s[end]!=' ':end = end-1return start-endclass Solution:def lengthOfLastWord(self, s: str) -> int:n = len(s)start = n-1end = n-1while end>=0 and s[end]==' ':end = end-1start = endwhile end>=0 and s[end]!=' ':end = end-1return start-end

89. 合并两个有序数组

利用双指针从前到后进行归并排序。
题目中给出了有效数字的概念，牢记指针边界与有效数字位数的关系，比较简单的一道排序问题。

！：可以使用双指针从后向前，避免了开辟额外空间存储数组。因为已知nums1的长度为m+n，直接逆序存储元素，可以直接插入。

# 从前向后的双指针
# 直接双指针的归并排序，当一个遍历结束，剩下的全部加到队列末尾
class Solution:def merge(self, nums1: List[int], m: int, nums2: List[int], n: int) -> None:"""Do not return anything, modify nums1 in-place instead."""ans = []i,j = 0,0while(i<m and j<n):if (nums1[i]<=nums2[j]):ans.append(nums1[i])i = i+1else:ans.append(nums2[j])j = j+1if j<n:ans = ans + nums2[j:n]elif i<m:ans = ans + nums1[i:m]nums1[:] = ans# 从后向前的双指针,精彩！
class Solution:def merge(self, nums1: List[int], m: int, nums2: List[int], n: int) -> None:"""Do not return anything, modify nums1 in-place instead."""ans = []i,j = m-1, n-1p = m + n - 1while i>=0 and j>=0:if nums1[i]<=nums2[j]:nums1[p] = nums2[j]j = j-1else:nums1[p] = nums1[i]i = i-1p = p-1if j>=0:nums1[:j+1] = nums2[:j+1]

125. 验证回文串

只要考察对于语言字符串相关API的应用与理解：

capitalize()
将字符串的第一个字符转换为大写
center(width, fillchar)
返回一个指定的宽度 width 居中的字符串，fillchar 为填充的字符，默认为空格。
count(str, beg= 0,end=len(string))
返回 str 在 string 里面出现的次数，如果 beg 或者 end 指定则返回指定范围内 str 出现的次数
encode(encoding=‘UTF-8’,errors=‘strict’)
以 encoding 指定的编码格式编码字符串，如果出错默认报一个ValueError 的异常，除非 errors 指定的是’ignore’或者’replace’
endswith(suffix, beg=0, end=len(string))
检查字符串是否以 obj 结束，如果beg 或者 end 指定则检查指定的范围内是否以 obj 结束，如果是，返回 True,否则返回 False.
find(str, beg=0, end=len(string))
检测 str 是否包含在字符串中，如果指定范围 beg 和 end ，则检查是否包含在指定范围内，如果包含返回开始的索引值，否则返回-1
index(str, beg=0, end=len(string))
跟find()方法一样，只不过如果str不在字符串中会报一个异常。
isalnum()
如果字符串至少有一个字符并且所有字符都是字母或数字则返回 True，否则返回 False
isalpha()
如果字符串至少有一个字符并且所有字符都是字母或中文字则返回 True, 否则返回 False
isdigit()
如果字符串只包含数字则返回 True 否则返回 False…
islower()
如果字符串中包含至少一个区分大小写的字符，并且所有这些(区分大小写的)字符都是小写，则返回 True，否则返回 False
isnumeric()
如果字符串中只包含数字字符，则返回 True，否则返回 False
isspace()
如果字符串中只包含空白，则返回 True，否则返回 False.
isupper()
如果字符串中包含至少一个区分大小写的字符，并且所有这些(区分大小写的)字符都是大写，则返回 True，否则返回 False
join(seq)
以指定字符串作为分隔符，将 seq 中所有的元素(的字符串表示)合并为一个新的字符串
len(string)
返回字符串长度
ljust(width[, fillchar])
返回一个原字符串左对齐,并使用 fillchar 填充至长度 width 的新字符串，fillchar 默认为空格。
lower()
转换字符串中所有大写字符为小写.
lstrip()
截掉字符串左边的空格或指定字符。
maketrans()
创建字符映射的转换表，对于接受两个参数的最简单的调用方式，第一个参数是字符串，表示需要转换的字符，第二个参数也是字符串表示转换的目标。
max(str)
返回字符串 str 中最大的字母。
min(str)
返回字符串 str 中最小的字母。
replace(old, new [, max])
将字符串中的 old 替换成 new,如果 max 指定，则替换不超过 max 次。
rfind(str, beg=0,end=len(string))
类似于 find()函数，不过是从右边开始查找.
rindex( str, beg=0, end=len(string))
类似于 index()，不过是从右边开始.
rjust(width,[, fillchar])
返回一个原字符串右对齐,并使用fillchar(默认空格）填充至长度 width 的新字符串
rstrip()
删除字符串字符串末尾的空格.
split(str="", num=string.count(str))
以 str 为分隔符截取字符串，如果 num 有指定值，则仅截取 num+1 个子字符串
splitlines([keepends])
按照行(’r’, ‘rn’, n’)分隔，返回一个包含各行作为元素的列表，如果参数 keepends 为 False，不包含换行符，如果为 True，则保留换行符。
startswith(substr, beg=0,end=len(string))
检查字符串是否是以指定子字符串 substr 开头，是则返回 True，否则返回 False。如果beg 和 end 指定值，则在指定范围内检查。
strip([chars])
在字符串上执行 lstrip()和 rstrip()
swapcase()
将字符串中大写转换为小写，小写转换为大写
translate(table, deletechars="")
根据 str 给出的表(包含 256 个字符)转换 string 的字符, 要过滤掉的字符放到 deletechars 参数中
upper()
转换字符串中的小写字母为大写
zfill (width)
返回长度为 width 的字符串，原字符串右对齐，前面填充0
isdecimal()
检查字符串是否只包含十进制字符，如果是返回 true，否则返回 false。

方法：

筛选+判断对称 (翻转、双指针)
原字符串上使用双指针

# 方法1，筛选+翻转
class Solution:def isPalindrome(self, s: str) -> bool:n = [i.lower() for i in s if i.isalnum()]return n==n[::-1]
# 方法2，双指针
class Solution:def isPalindrome(self, s: str) -> bool:start = 0end = len(s)-1while start<end:while start<end and not s[start].isalnum():start += 1while start<end and not s[end].isalnum():end -= 1if start<end: if s[start].lower()!=s[end].lower():return Falsestart += 1end -= 1return True

141. 环形链表

167. 两数之和 ||

left+right>target ，需要right左移，减少两数和
left+right<target，需要left右移，增大两数和

class Solution:def twoSum(self, numbers: List[int], target: int) -> List[int]:left = 0right = len(numbers)-1while left<right:if numbers[left]+numbers[right]==target:return [left+1, right+1]elif numbers[left]+numbers[right]>target:right -= 1elif numbers[left]+numbers[right]<target:left += 1

228. 汇总区间

解法：

简单一次遍历（while）。遍历的过程中需要考虑到边界的问题，很重要。
双指针（for），逐次更新start指针和end指针。

# 必须要遍历到i=length-1处，此时i+1超出了数组范围，
# 必须要处理好边界问题
class Solution:def summaryRanges(self, nums: List[int]) -> List[str]:length = len(nums)i = 0summary = []while i < length:start = nums[i]while i<length-1 and nums[i+1]==nums[i]+1:i = i+1end = nums[i]i = i + 1if start==end:summary.append(str(start))else:summary.append(str(start)+'->'+str(end))return summaryclass Solution:def summaryRanges(self, nums: List[int]) -> List[str]:length = len(nums)i = 0summary = []while i < length:start = nums[i]i = i+1while i<length and nums[i]==nums[i-1]+1:i = i+1end = nums[i-1]if start==end:summary.append(str(start))else:summary.append(str(start)+'->'+str(end))return summary

双指针：

class Solution:def summaryRanges(self, nums: List[int]) -> List[str]:length = len(nums)summary = []start = 0 # 双指针依次更新双指针for i in range(0,length):if i+1>=length or nums[i]+1!=nums[i+1]:end = iif start==end:summary.append(str(nums[start]))else:summary.append(str(nums[start])+'->'+str(nums[end])) start = i+1return summary

查找及插入问题

二分查找及其变种

二分查找的核心思想是「减而治之」，即「不断缩小问题规模」。
二分查找的两种思路：

思路 1：在循环体内部查找元素，搜索一个元素时，左闭右闭，直接看if是否相同，相同时返回；while结束返回-1.
while(left <= right) 这种写法表示在循环体内部直接查找元素；
退出循环的时候 left 和 right 不重合，区间 [left, right] 是空区间。
思路 2：在循环体内部排除元素（重点），搜索左右边界，此时搜索区间左闭右开，if相等时不返回，用mid确定新边界；
while(left < right) 这种写法表示在循环体内部排除元素；
退出循环的时候 left 和 right 重合，区间 [left, right] 只剩下成 11 个元素，这个元素有可能就是我们要找的元素。

探究几个最常用的二分查找场景：寻找一个数、寻找左侧边界、寻找右侧边界。而且，我们就是要深入细节，比如不等号是否应该带等号，mid 是否应该加一等等。分析这些细节的差异以及出现这些差异的原因，保证你能灵活准确地写出正确的二分查找算法。
链接: Leetcode.
链接: Leetcode.

模板

# 模板  ...表示需要注意的地方
int binarySearch(int[] nums, int target) {int left = 0, right = ...;  # 表示了区间的开闭while(...) {int mid = left + (right - left) / 2;if (nums[mid] == target) {...} else if (nums[mid] < target) {left = ...} else if (nums[mid] > target) {right = ...}}return ...;
}

寻找一个数的二分搜索（基本的二分搜索）

int binarySearch(int[] nums, int target) {int left = 0; int right = nums.length - 1; // 注意，左闭右闭while(left <= right) {int mid = left + (right - left) / 2;if(nums[mid] == target)return mid; else if (nums[mid] < target)left = mid + 1; // 注意else if (nums[mid] > target)right = mid - 1; // 注意}return -1;
}

寻找左边界的二分搜索

// 寻找左边界的关键其实是寻找当前列表中多少数小于targe
// 所以使用左闭右开区间，当if条件达成，不返回，不断向左收缩
// 在新区间里找target，可以确定左边界
// 左闭右开，所以right = length，右边界取不到，
// 所以直接right=mid，而无需right = mid-1
int left_bound(int[] nums, int target) {if (nums.length == 0) return -1;int left = 0;int right = nums.length; // 注意while (left < right) { // 注意int mid = (left + right) / 2;if (nums[mid] == target) {right = mid;  //此时左边界一定在mid左侧或者mid，所以right=mid} else if (nums[mid] < target) {left = mid + 1;} else if (nums[mid] > target) {right = mid; // 注意}}// target 比所有数都大if (left == nums.length) return -1;// 类似之前算法的处理方式return nums[left] == target ? left : -1;
}// 修改的左闭右闭代码
int left_bound(int[] nums, int target) {int left = 0, right = nums.length - 1;// 搜索区间为 [left, right]while (left <= right) {int mid = left + (right - left) / 2;if (nums[mid] < target) {// 搜索区间变为 [mid+1, right]left = mid + 1;} else if (nums[mid] > target) {// 搜索区间变为 [left, mid-1]right = mid - 1;} else if (nums[mid] == target) {// 收缩右侧边界right = mid - 1;}}// 检查出界情况if (left >= nums.length || nums[left] != target)return -1;return left;
}

寻找右边界的二分搜索

int right_bound(int[] nums, int target) {if (nums.length == 0) return -1;int left = 0, right = nums.length;while (left < right) {int mid = (left + right) / 2;if (nums[mid] == target) {left = mid + 1; // 注意} else if (nums[mid] < target) {left = mid + 1;} else if (nums[mid] > target) {right = mid;}}return left - 1; // 注意
}

33. 搜索旋转排序数组

35. 搜索插入位置

方法：

直接遍历
二分查找（在一个有序列表中查找，二分查找以O（log n）时间复杂度完成搜索，但是在这个任务中，二分查找法需要对条件进行修改，即我们需要：在一个有序数组中找第一个大于等于 target 的下标）

class Solution:def searchInsert(self, nums: List[int], target: int) -> int:low = 0high = len(nums)-1while low<=high:mid = (low+high)//2if nums[mid]==target:return midelif nums[mid]<target:low = mid + 1elif nums[mid]>target:high = mid-1if target>nums[mid]: # 在mid后插入，插入位置为mid+1return mid+1else:   # 在mid出插入return mid# 优化后代码
class Solution:def searchInsert(self, nums: List[int], target: int) -> int:low = 0high = len(nums)-1ans = 0while low<=high:mid = (low+high)//2if nums[mid]>=target:ans = midhigh = mid-1else:  # 严格小于 target 的元素一定不是解low = mid + 1return ans

69. x的平方根

方法：

「袖珍计算器算法」是一种用指数函数 exp 和对数函数 ln 代替平方根函数的方法。我们通过有限的可以使用的数学函数，得到我们想要计算的结果。
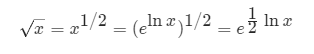
二分查找。在一个有范围的区间里搜索一个整数。
牛顿迭代法

# 方法一
class Solution:def mySqrt(self, x: int) -> int:if x == 0:return 0ans = int(math.exp(0.5 * math.log(x)))return ans + 1 if (ans + 1) ** 2 <= x else ans
# 方法二
# 整个问题可以转化为，平方小于等于x的最大整数
# 如果选择右边界，决定了迭代次数，最大可以选择x-1；对于x>4，可以选择x//2
class Solution:def mySqrt(self, x: int) -> int:import mathleft = 0right = math.ceil(x/2)ans = 0while left<=right:mid = (left+right)//2if mid*mid <= x:ans = midleft = mid+1elif mid*mid > x:right = mid - 1return ans
# 0 1 2 3 4
# mid 2  left = mid+1 = 3 --> mid 3 right = 2# 方法三 牛顿迭代法
# 函数f(x) = ans^2 - x，求f(x)=0时的ans，即求出使f(x)逼近0的最优解
# 导数f'(x) = 2*ans
class Solution:def mySqrt(self, x: int) -> int:if x == 0:return 0C, x0 = float(x), float(x)while True:xi = 0.5 * (x0 + C / x0)if abs(x0 - xi) < 1e-7:breakx0 = xireturn int(x0)

153. 寻找旋转排序数组中的最小值

本质就是一个寻找降序断点的问题，查找降序位置。遍历查找的话时间复杂度受到数组长度的影响，在数组的查找问题上可以使用二分法。
思路一：
直接查找出现下降的区间，确定二分查找的条件，即当mid<left时，唯一的下降区间出现在[left,mid]，mid可能对应最小值位置；当mid>right时，唯一的下降区间出现在[mid+1,right]，此时mid不可能对应最小值位置。因为不存在相同元素，所以在元素数>2时，mid的值永远满足以上两种情况。而当mid与left重合时，此时区间只有两个值，直接返回两个值中的最小值。

思路二：

考虑数组中的最后一个元素 x：在最小值右侧的元素（不包括最后一个元素本身），它们的值一定都严格小于 x；而在最小值左侧的元素，它们的值一定都严格大于 x。因此，我们可以根据这一条性质，通过二分查找的方法找出最小值。

在二分查找的每一步中，左边界为low，右边界为high，区间的中点为pivot，最小值就在该区间内。我们将中轴元素 nums[pivot] 与右边界元素 nums[high] 进行比较，可能会有以下的三种情况：

第一种情况是 nums[pivot]<nums[high]。如下图所示，这说明 nums[pivot] 是最小值右侧的元素，因此我们可以忽略二分查找区间的右半部分。
第二种情况是 nums[pivot]>nums[high]。如下图所示，这说明 nums[pivot] 是最小值左侧的元素，因此我们可以忽略二分查找区间的左半部分。
由于数组不包含重复元素，并且只要当前的区间长度不为 1，pivot 就不会与 high 重合；而如果当前的区间长度为 1，这说明我们已经可以结束二分查找了。因此不会存在 nums[pivot]=nums[high] 的情况。

# 思路一：
class Solution:def findMin(self, nums: List[int]) -> int:left = 0right = len(nums)-1while left<right:mid = left + (right-left)//2if nums[mid]<nums[left]:right = midelif nums[mid]>nums[right]:left = mid+1else:return min(nums[left], nums[right])return nums[left]# 思路二
class Solution:def findMin(self, nums: List[int]) -> int:    low, high = 0, len(nums) - 1while low < high:pivot = low + (high - low) // 2if nums[pivot] < nums[high]:high = pivot else:low = pivot + 1return nums[low]

704. 二分查找

在数组中查找符合条件的元素的下标。

class Solution:def search(self, nums: List[int], target: int) -> int:low = 0high = len(nums)-1while(low<=high):  # 查找的时候需要使用=，否则会漏掉最终一个边界元素，# 即mid=low=high对应的元素，返回（low，high）为空# mid = (low+high)//2 # mid向下或者向上取整常规状态下不影响结果mid = low + (high - low) // 2  # 避免left和right很大的时候溢出，python不存在这个问题if nums[mid]==target:return midif nums[mid]>target:high = mid - 1if nums[mid]<target:low = mid + 1return -1
#如果非要使用low<high，则return nums[left] == target ? left : -1;

852. 山脉数组的峰顶索引

方法：

线性扫描，当arr[i]>arr[i+1]时，i即为峰顶
二分查找，这个题目中二分查找的关键在于左移右移的条件选择，当arr[mid]<arr[mid+1]，证明还在爬山，移动左指针；当arr[mid]>arr[arr+1]，证明在下山，移动右指针。细节的把控上需要仔细思考和调控。

# 方法一
// A code block
var foo = 'bar';# 方法二
class Solution:def peakIndexInMountainArray(self, arr: List[int]) -> int:length = len(arr)left = 0right = length-1ans = 0while left<=right:mid = (left+right)//2if arr[mid]<arr[mid+1]:left = mid + 1elif arr[mid]>arr[mid+1]:right = mid-1ans = midreturn ans

队列、栈

155. 最小栈

考察栈的基本概念，熟练掌握list（python）、数组（c/c++）的相关操作，可以轻松解决该简单题。问题的难度在于如何在常数时间内检索到最小元素的栈。自然地，我们如果能够在每次push新元素进入时，保存当前栈状态下对应的最小元素；那么当我们查询最小元素时，可以直接返回最小元素值。

建立辅助栈minStack来存储最小元素，与元素栈同步插入与删除，用于存储与每个元素对应的最小值。当push新元素x进入Stack时，min(minStack[-1],x)为当前栈状态下的最小元素，push进minStack中。

class MinStack:def __init__(self):"""initialize your data structure here."""self.Stack = []self.minStack = [float(inf)]def push(self, x: int) -> None:self.Stack.append(x)self.minStack.append(min(self.minStack[-1], x))def pop(self) -> None:self.Stack.pop()self.minStack.pop()def top(self) -> int:return self.Stack[-1]def getMin(self) -> int:return self.minStack[-1]

同样的思路，我们可以不使用两个栈来进行操作，而只使用一个栈来保存。当有更小的值来的时候，我们只需要把之前的最小值入栈，当前更小的值再入栈即可。当这个最小值要出栈的时候，下一个值便是之前的最小值了。

入栈 2 ，同时将之前的 min 值 3 入栈，再把 2 入栈，同时更新 min = 2
| 2 |   min = 2
| 3 |  
| 5 |     
|_3_|    
stack  入栈 6 
| 6 |  min = 2
| 2 |   
| 3 |  
| 5 |     
|_3_|    
stack  出栈 6     
| 2 |   min = 2
| 3 |  
| 5 |     
|_3_|    
stack  出栈 2     
| 2 |   min = 2
| 3 |  
| 5 |     
|_3_|    
stack  出栈 2     
|   |  min = 3   
| 5 |   
|_3_|    
stack

class MinStack:def __init__(self):"""initialize your data structure here."""self.Stack = []self.min = float(inf)def push(self, x: int) -> None:if x<=self.min:  # 加入这个元素更新了最小值，则将之前的最小值保存self.Stack.append(self.min)self.min = xself.Stack.append(x)def pop(self) -> None:a = self.Stack.pop()if a == self.min:self.min = self.Stack.pop()def top(self) -> int:return self.Stack[-1]def getMin(self) -> int:return self.min

这种方法会使用额外的空间来存储，怎么样能不使用额外空间？
我们使用一个变量存储min，在每次存入元素x的时候，每次存入 x-min。

当存入值为正时，则x大于min，不更新min，当从栈中pop元素时，输出 x-min+min；
当存入值为负时，则更新min=x，在pop过程中每次pop出负数，则证明修改过min，将min改为min-存入值。

入栈 3，存入 3 - 3 = 0
|   |   min = 3
|   |     
|_0_|    
stack   入栈 5，存入 5 - 3 = 2
|   |   min = 3
| 2 |     
|_0_|    
stack  入栈 2，因为出现了更小的数，所以我们会存入一个负数，这里很关键
也就是存入  2 - 3 = -1, 并且更新 min = 2 
对于之前的 min 值 3, 我们只需要用更新后的 min - 栈顶元素 -1 就可以得到    
| -1|   min = 2
| 5 |     
|_3_|    
stack  入栈 6，存入  6 - 2 = 4
| 4 |   min = 2
| -1| 
| 5 |     
|_3_|    
stack  出栈，返回的值就是栈顶元素 4 加上 min，就是 6
|   |   min = 2
| -1| 
| 5 |     
|_3_|    
stack  出栈，此时栈顶元素是负数，说明之前对 min 值进行了更新。
入栈元素 - min = 栈顶元素，入栈元素其实就是当前的 min 值 2
所以更新前的 min 就等于入栈元素 2 - 栈顶元素(-1) = 3
|   | min = 3
| 2 |     
|_0_|    
stack

class MinStack:def __init__(self):"""initialize your data structure here."""self.Stack = []self.min = float(inf)  # 仅使用一个变量表示mindef push(self, x: int) -> None:if len(self.Stack)==0: # 初始化栈时，push元素时栈顶为0self.Stack.append(0)self.min = xelse:self.Stack.append(x-self.min)if x<=self.min:  self.min = xdef pop(self) -> None:a = self.Stack.pop()  # 如果栈顶为负，则更新minif a < 0:self.min = self.min - adef top(self) -> int:# 当栈顶大于0时，则if self.Stack[-1]>=0:return self.Stack[-1]+self.minelse:    # 当前push值小于min时，将该值赋给min，栈顶为负数，用于恢复min# 当栈顶为负数时，则栈顶对应元素为min，直接返回minreturn self.mindef getMin(self) -> int:return self.min

895. 最大概率栈（Hard）

1、对于我来说最简单的思路就是，维护两个哈希表，其中一个来保存频率、一个作为常规栈来标识最靠近栈顶的元素。在保存频率的哈希表中，我们依次记录在当时的出现次数，当删除最大频率元素之后，每个对应元素对应的次数可以无需改变，只需要重新计算最大频率即可。在这个过程中，需要频繁地迭代，包括从队尾搜索元素索引，比较耗时。
当依次往栈中输入7，5，7，5，2，7时，对应的频率为 1 1 2 2 1 3，在push和pop的过程中按逻辑处理。

class FreqStack:def __init__(self):self.count = []self.stack = []def push(self, val: int) -> None:if val not in self.stack:self.count.append(1)self.stack.append(val)else:self.stack.append(val)count = 0for i in self.stack:if i == val:count += 1self.count.append(count)def pop(self) -> int:count_max = max(self.count)for i in range(len(self.count)-1,-1,-1):if count_max == self.count[i]:del self.count[i]m = self.stack[i]del self.stack[i]return m

2、第二种思路是将栈维护成一个字典，字典的key值为频率，value值为保存了对应出现次数的元素，同时可以标记出栈顶位置，只需要根据最大频率，从对应的value中取出元素，当对应的value为空时，则直接调整最大频率。

class FreqStack:def __init__(self):self.count = {}self.stack = collections.defaultdict(list)self.maxcount = 0def push(self, val: int) -> None:self.count[val] = self.count.get(val, 0) + 1if self.count[val] > self.maxcount:self.maxcount = self.count[val]self.stack[self.count[val]].append(val)def pop(self) -> int:res = self.stack[self.maxcount].pop()self.count[res] -= 1if not self.stack[self.maxcount]:self.maxcount -= 1return res

单调栈

42. 蓄水池

84. 柱状图中的最大矩形

496. 下一个更大元素|

738. 每日温度

901. 股票价格跨度

数组

66. 加一

考虑对于基础数学加法原则和数组知识的考察，比较简单。

# 写法一，提前为数组补上首位0，可直接在原数组上修改，简化了首位赋值的困难
class Solution:def plusOne(self, digits: List[int]) -> List[int]:digits = [0]+digitsrex = 1n = len(digits)for i in range(n-1,-1,-1):num = digits[i] + rexif num>9:digits[i] = num%10rex = 1else:digits[i] = numbreakif digits[0]==0:return digits[1:]else:return digits# 写法二，
class Solution:def plusOne(self, digits: List[int]) -> List[int]:digits = digitsrex = 1n = len(digits)for i in range(n-1,-1,-1):num = digits[i] + rexif num>9:digits[i] = num%10rex = 1else:digits[i] = numreturn digitsreturn [1]+digits

67. 二进制求和

末尾对齐，逐位相加，遇2进1。可以先反转这个代表二进制数字的字符串，然后低下标对应低位，高下标对应高位。当然你也可以直接把 aa 和 bb 中短的那一个补 0 直到和长的那个一样长，然后从高位向低位遍历。
如果循环结束，进位为1，则前补’1’

class Solution:def addBinary(self, a: str, b: str) -> str:ret = 0  # 记录进位na = len(a)nb = len(b)c =''if na>nb:b = '0'*(na-nb)+bmn = naelif na<nb:a = '0'*(nb-na)+amn = nbelse:mn = nafor i in range(mn-1,-1,-1):num = int(a[i])+int(b[i]) + retif num>1:num_ = num%2ret = num//2c = str(num_)+celse:ret = 0c = str(num)+cif ret==1:return '1'+celse:return c

189. 旋转数组 middle

class Solution:def rotate(self, nums: List[int], k: int) -> None:"""Do not return anything, modify nums in-place instead."""length = len(nums)k = k % length # 如果k大于length，需要取余，以提取出最后的元素#方法零 开新数组，将元素放在对应位置上# new = [0]*length# for i in range(length):# new[(i+k)%length] = nums[i]# nums[:] = new# 方法一 因为环形循环，保留会被覆盖的k个元素,这也开辟了新空间，直接循环移动# if k==0:#     pass# else:#     tmp = nums[-k:]#     for j in range(length-k-1, -1, -1):#         nums[j+k] = nums[j]#     nums[:k] = tmp# 方法二  循环问题，可以直接在后面开一个相同的数组，直接通过数学计算确定开始位置和结束位置，但是这样开了额外空间。#不写切片相当于nums修改的地址重新指向右边的临时地址，写切片相当于按着切片下标修改值，前者在线上判定里无法AC，线上判定只判定原地地址的情况，不写切片的nums只在函数内有效。# new_nums = nums+nums# start = length-k# end = 2*length - k# nums[:] = new_nums[start:end:1]  # [:]代表取元素再赋值，而不是直接变更nums数组# nums[: ] = (nums[i] for i in range(-(k % len(nums)), len(nums) - k % len(nums)))# 方法三 翻转法，依旧未开辟额外空间,python list自带deverse()函数# 我们可以采用翻转的方式，比如12345经过翻转就变成了54321，这样已经做到了把前面的数字放到后面去，但是还没有完全达到我们的要求，比如，我们只需要把12放在后面去，目标数组就是34512，与54321对比发现我们就只需要在把分界线前后数组再进行翻转一次就可得到目标数组了。所以此题只需要采取三次翻转的方式就可以得到目标数组，首先翻转分界线前后数组，再整体翻转一次即可。# def reverse(nums, start, end):#     while start<=end:#         temp = nums[start]#         nums[start] = nums[end]#         nums[end] = temp#         start = start+1#         end = end-1# reverse(nums,0,length-1)# reverse(nums,0, k-1)# reverse(nums,k,length-1)# 方法四 循环替换import mathn, k = len(nums), k % len(nums)g = math.gcd(k, n)for i in range(g):s, x = i, nums[i]for j in range(n // g):nums[(s + k) % n], x = x, nums[(s + k) % n]s = (s + k) % n

560. 和为k的子数组

# 直接暴力求解，依次遍历左边界和右边界，累计求和，时间复杂度为O(n^2)
# 使用一个数组pre来存储从初始位置到当前位置的累加和，那么位置i和j之间子集的差值可以写成pre[j]-pre[i-1]==k，pre[i]+k==pre[j] (j>i)
# 如果该值等于k，则保存，相当于给定数组位置j处的元素，求j前面元素位置等于pre[j]-k的元素位置，等同于两数之和问题
# 使用哈希表，当遍历到位置j时，hash表中只存储了≤j元素位置的值，所以不会计算出来负值
import collections
class Solution:def subarraySum(self, nums: List[int], k: int) -> int:count = dict()num = 0length = len(nums)count[0] = 1pre = 0for i in range(length):pre += nums[i]if (pre-k) in count:num += count[(pre-k)]count[pre] = count.get(pre, 0) + 1return num

674. 最长连续递增序列

// A code block
var foo = 'bar';

链表

19. 删除链表的倒数第N个结点

# Definition for singly-linked list.
# class ListNode:
#     def __init__(self, val=0, next=None):
#         self.val = val
#         self.next = next
class Solution:def removeNthFromEnd(self, head: ListNode, n: int) -> ListNode:# 可以直接遍历整个数组记录数组长度# new_head = ListNode(0, head)# count = 0# while head:#     head = head.next#     count += 1# j = 0# curr = new_head# while j< count-n:#     curr = curr.next#     j += 1# curr.next = curr.next.next# return new_head.next# 只遍历一次的情况下，可以以空间换时间# new_head = ListNode(0, head)# re = []# curr = new_head# while curr:#     re.append(curr)#     curr = curr.next# node = re[-n-1]# node.next = node.next.next# return new_head.next# 双指针可以在常数空间中解决问题，只需要维护一个间隔为n的双指针，当快指针为Null时，此时慢指针为需要删除的元素dummy = ListNode(0, head)first = headsecond = dummyfor i in range(n):first = first.nextwhile first:first = first.nextsecond = second.nextsecond.next = second.next.nextreturn dummy.next

83. 删除排序链表中的重复元素(hash)

# 用hash存储元素，重点考察hash的应用以及链表的基本操作
# 当该结点元素重复时，需要将该结点前结点.next = curr.next，故需要保存前一个结点
class Solution:def deleteDuplicates(self, head: ListNode) -> ListNode:hash_list = set()curr = headwhile curr:val = curr.valif val not in hash_list:hash_list.add(val)pre = currcurr = curr.nextelse:pre.next = curr.nextcurr = pre.nextreturn head

138. 复制带随机指针的链表

141. 环形链表

# Definition for singly-linked list.
# class ListNode:
#     def __init__(self, x):
#         self.val = x
#         self.next = None
# 检测链表是否闭环，使用快慢指针
class Solution:def hasCycle(self, head: ListNode) -> bool:if head==None or head.next==None:return Falsefast = headslow = headwhile fast.next!=None and fast.next.next!=None:fast = fast.next.nextslow = slow.nextif fast==slow:return Truereturn False

160. 相交链表

方法：

暴力法：对链表A中的每一个结点a，遍历整个链表 B 并检查链表 B 中是否存在结点和 a相同。
哈希表法：遍历链表 A 并将每个结点的地址/引用存储在哈希表中。然后检查链表 B 中的每一个结点 b 是否在哈希表中。若在，则 b 为相交结点。
双指针法：创建两个指针 pApA 和 pBpB，分别初始化为链表 A 和 B 的头结点。然后让它们向后逐结点遍历。
当 pA到达链表的尾部时，将它重定位到链表 B 的头结点; 类似的，当 pB到达链表的尾部时，将它重定位到链表 A 的头结点。

假设pA和pB走完了全程：

由于指针pA走了个A+B，指针pB走了个B+A，因此两者走过的长度是相等的
A和B结尾部分是相等的，因此A+B和B+A结尾部分也是相等的
因此当pA与pB相遇时，该节点就是相交节点

假设A和B没有交点

A和B均是以null结尾，因此A+B和B+A也是以null结尾
因此当pA和pB恰好走完全程后，他们同时到达null，此时他们是相等的
依然满足循环终止条件

# 忽略了可以通过链接解决长度差问题，保证A、B指针同时到达相交结点，关键思路在于路径的构思
# A、B两链表到达链尾之后，再走到彼此的路，可以实现相同的路径长度
# 需要考虑的特殊情况，
# 设相交后长度为C，每个指针走过路程均为 A+B-C，如果存在相交结点则同时到达
# 相同长度不想交，在第一轮时同时到达None，退出
# 不同长度不想交，在第二轮时走过的长度均为A+B，同时到达None，退出，即使A或者B为None，走过路径依旧相同
class Solution:def getIntersectionNode(self, headA: ListNode, headB: ListNode) -> ListNode:A = headAB = headBwhile headA!=headB:headA = B if headA==None else headA.nextheadB = A if headB==None else headB.nextreturn headA

203. 移除链表元素

哨兵节点广泛应用于树和链表中，如伪头、伪尾、标记等，它们是纯功能的，通常不保存任何数据，其主要目的是使链表标准化，如使链表永不为空、永不无头、简化插入和删除。

# 解决链表问题的一个关键思路就是人为造一个初始结点，用以处理head
# 特殊情况：链表为空，删除节点为头结点，删除节点为最后一个结点
# 可以设置pre和curr，用两个结点完成删除操作
class Solution:def removeElements(self, head: ListNode, val: int) -> ListNode:mem = ListNode(float(inf))mem.next = headprev, curr = mem, headwhile curr:if curr.val==val:prev.next = curr.nextelse:prev = currcurr = curr.nextreturn mem.next
# 也可以每次访问curr.next.val，使用一个结点来完成删除操作
class Solution:def removeElements(self, head: ListNode, val: int) -> ListNode:mem = ListNode(float(inf))mem.next = headmem_ = memwhile mem.next!=None:if mem.next.val==val:mem.next = mem.next.nextelse:mem = mem.nextreturn mem_.next

树

100. 相同的树（递归）

# 递归调用，遍历左右子树，完整递归终止条件是，pq均为空（即遍历到叶子节点的左右子树），则正常终止此次递归
# 提前终止递归，p.val/q.val不同，q/p不同时为
class Solution:def isSameTree(self, p: TreeNode, q: TreeNode) -> bool:if p==None and q==None: return Trueif p!=None and q==None: return Falseif p==None and q!=None: return Falseif p.val!=q.val: return Falsereturn self.isSameTree(p.left, q.left) & self.isSameTree(p.right, q.right)

101. 对称二叉树

// A code block
var foo = 'bar';

104. 二叉树的最大深度

// A code block
var foo = 'bar';

107. 二叉树的层序遍历 ||

// A code block
var foo = 'bar';

108. 将有序数组转换为二叉搜索树（递归）

直观地看，我们可以选择中间数字作为二叉搜索树的根节点，这样分给左右子树的数字个数相同或只相差 11，可以使得树保持平衡。如果数组长度是奇数，则根节点的选择是唯一的，如果数组长度是偶数，则可以选择中间位置左边的数字作为根节点或者选择中间位置右边的数字作为根节点，选择不同的数字作为根节点则创建的平衡二叉搜索树也是不同的。

确定平衡二叉搜索树的根节点之后，其余的数字分别位于平衡二叉搜索树的左子树和右子树中，左子树和右子树分别也是平衡二叉搜索树，因此可以通过递归的方式创建平衡二叉搜索树。

递归的基准情形是平衡二叉搜索树不包含任何数字，此时平衡二叉搜索树为空。
树的遍历的终止条件，通常判定当前node为空，即为叶子节点的左右子树；而不是在叶子节点终止。
方法：

直接递归调用自身，每次传入新的数组序列
定义递归子函数，执行递归，只需要传入建树元素在数组序列中的位置

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None
# 方法一
class Solution:def sortedArrayToBST(self, nums: List[int]) -> TreeNode:if not nums:return Noneleft = 0right = len(nums)-1mid = left + (right-left)//2node = TreeNode(nums[mid])node.left = self.sortedArrayToBST(nums[:mid])node.right = self.sortedArrayToBST(nums[mid+1:])return node# 方法二
class Solution:def sortedArrayToBST(self, nums: List[int]) -> TreeNode:def helper(left, right):if left > right:return None# 总是选择中间位置左边的数字作为根节点mid = (left + right) // 2root = TreeNode(nums[mid])root.left = helper(left, mid - 1)root.right = helper(mid + 1, right)return rootreturn helper(0, len(nums) - 1)

110. 平衡二叉树

// A code block
var foo = 'bar';

111. 二叉树的最小深度

// A code block
var foo = 'bar';

112. 路径总和

查找到叶子节点的路径和，可以使用DFS或者BFS。

在使用DFS中，需要记录到当前位置的和sum，再遍历左右子树，遍历左子树之后，去遍历右子树的时候很自然地希望当前位置的和依旧为sum。
在实际代码中方法：

回溯法，当从dfs退出时，sum减去当前结点的val
形参法，不定义变量，每次传入sum+val，避免了sum的修改

使用广度优先搜索BFS的方式，记录从根节点到当前节点的路径和，以防止重复计算。这样我们使用两个队列，分别存储将要遍历的节点，以及根节点到这些节点的路径和即可。

DFS：

# 询问是否有从「根节点」到某个「叶子节点」经过的路径上的节点之和等于目标和。
#核心思想是对树进行一次遍历，在遍历时记录从根节点到当前节点的路径和，以防止重复计算。
# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = Noneclass Solution:def hasPathSum(self, root: TreeNode, sum: int) -> bool:if root ==None:return Falsedef dfs(node, sum_):if node.left==None and node.right==None:if sum==sum_+node.val:return Trueelse:return Falseresult_1 = Falseresult_2 = Falseif node.left:result_1 = dfs(node.left, sum_+node.val)if node.right:result_2 = dfs(node.right, sum_+node.val)return result_1 or result_2# 使用or的一个好处就是当前面判定为True，则直接返回，不进行or后的计算return dfs(root, 0)

BFS：

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = Noneclass Solution:def hasPathSum(self, root: TreeNode, sum: int) -> bool:if not root:return Falseval_list = [root.val]node_list = [root]while node_list:node = node_list.pop(0)value = val_list.pop(0)if node.left==None and node.right==None:if value == sum:return Trueif node.left:node_list.append(node.left)val_list.append(value+node.left.val)if node.right:node_list.append(node.right)val_list.append(value+node.right.val)return False

动态规划

53. 最大子序和

方法：

暴力求解，直接遍历，O（n^2）时间复杂度
暴力解法的思路，第一层for 就是设置起始位置，第二层for循环遍历数组寻找最大值
贪心，与暴力求解中依次回到初始元素，贪心每次作出当前的最优选择。为了贪心地追求局部最优：当前“连续和”为负数的时候立刻放弃，从下一个元素重新计算“连续和”，因为负数加上下一个元素 “连续和”只会越来越小。局部最优的情况下，并记录最大的“连续和”，可以推出全局最优。从代码角度上来讲：遍历nums，从头开始用count累积，如果count一旦加上nums[i]变为负数，那么就应该从nums[i+1]开始从0累积count了，因为已经变为负数的count，只会拖累总和。这相当于是暴力解法中的不断调整最大子序和区间的起始位置。
首先永远从非负整数开始，在当前元素加到sum的时候，保留最大值；当sum小于0时，在之后不可能出现最大子序列和，将sum置0.
动态规划，若前一个元素大于0，则加在当前元素上。

问题演化为求f(0)–f(n-1)的最大值，根据动态规划转移方程，如果要求f(n-1)，首先要依次求f(0) f(1) f(2)……，而f(0)可以很轻易的被求出来，f(0) = nums[0]，直接通过迭代求解，并在过程中保留最大值。
而整个过程类似于贪心，当f(x)>0时，显然f(x)+a更大，继续向后推导；当f(x)<0时，等同于sum<0时重置sum=0，此时f(x+1) = 0+a。
分治

代码：

# 暴力求解，python不能AC，C++语言可以AC
class Solution:def maxSubArray(self, nums: List[int]) -> int:length = len(nums)max_ = nums[0]for i in range(length):sum_ = 0for j in range(i, length):sum_ = sum_ + nums[j]if sum_>max_:max_ = sum_return max_# 贪心
class Solution:def maxSubArray(self, nums: List[int]) -> int:import mathmax_ = -float('inf')sum_ = 0length = len(nums)for i in range(length):sum_ = sum_+nums[i]max_ = max(max_, sum_)if sum_<0:sum_ = 0return max_                   
# 动态规划
class Solution:def maxSubArray(self, nums: List[int]) -> int:f = nums[0]n = len(nums)max_ = nums[0]for i in range(1,n):f = max(f+nums[i], nums[i])max_ = max(f, max_)return max_

70. 爬楼梯

方法：

典型的动态规划问题，使用dp数组或者滚动数组
根据数学规律总结通项公式
递归；记忆化递归：可以保存中间结果，减少重复计算

# 动态规划，设f(x)为爬x阶到达楼顶的不同方法次数
# 状态方程！
# f(n) = f(n-1) + f(n-2)
# f(0) = 1
# f(1) = 1
# f(2) = f(1)+f(0) =2
# f(3) = f(2)+f(1) =3
# f(4) = f(3)+f(2) =5
class Solution:def climbStairs(self, n: int) -> int:f_1 = 1f_2 = 1for i in range(1,n):f = f_1 + f_2  # 滚动数组，斐波那契数列f_2 = f_1f_1 = freturn f_1

121. 买卖股票的最佳时机 |

与55. 最大子序和相同类似
方法：

暴力求解，遍历数组，选择买入日期，在之后的序列中选择卖出日期，保留最大收益，O(n^2)。

# 暴力法无法AC，样例测试超市
// A code block
var foo = 'bar';

贪心，双指针：使用start和end标记当前买入和卖出日期，当prices[end]-prices[start]小于0时，即出现了更低的买入价格，我们从新的买入价格之后查找卖

# 贪心+双指针：一旦出现负数收益，即出现了更小的买入价格，更新买入价格
class Solution:def maxProfit(self, prices: List[int]) -> int:ans = 0start = 0end = 1n = len(prices)while end<n:re = prices[end]-prices[start]if re<=0:start = endend = end+1else:ans = max(ans, re)end = end+1return ans# 贪心+一次遍历
class Solution:def maxProfit(self, prices: List[int]) -> int:ans = 0minprice = prices[0]n = len(prices)for i in range(1,n):if minprice>=prices[i]:minprice = prices[i]else:ans = max(ans, prices[i]-minprice)return ans

动态规划

122. 买卖股票的最佳时机 ||

class Solution:def maxProfit(self, prices: List[int]) -> int:start,end,ans = 0,1,0n = len(prices)while end<len(prices):while end<n and prices[end-1]<=prices[end]:end = end+1ans += prices[end-1]-prices[start]start = endend = start+1return ans

198. 打家劫舍

动态规划应该从终止条件往前推导，直到找到边界条件

垃圾的动态规划，使用了dp数组，假设从第i家偷到第j家的收益为f(i,j)
在这道题中边界条件为长度为1时，偷取该家得到最大收益
个人习惯从前往后推导，更像是贪心，反而使问题复杂化
如果选择该家盗窃，则无法盗窃i+1家，求第i+2家到第j家的最大收益
如果不选择该家盗窃，那么盗窃第i+1家，求第i+3家到第j家的最大收益
这里i+2与i+3会带来严重的边界问题，需要进行代码优化
f(i,j) = max(f(i,i)+f(i+2,j), f(i+1,i+1)+f(i+3, j))以[3,1,2,9]为例
f(1,1) = 3
f(1,2) = 3
f(1,3) = max(f(1,1)+f(3,3),f(2,2))=5
f(1,4) = max(f(1,1)+f(3,4),f(2,2)+f(4,4))=12
dp数组构建顺序：
f(4,4), f(3,3), f(3,4), f(2,2), f(2,3), f(2,4), f(1,1),f(1,2),f(1,3),f(1,4)

class Solution:def rob(self, nums: List[int]) -> int:n = len(nums)if n==0:return 0dp = [[0 for _ in range(n)] for _ in range(n)]for i in range(n-1, -1, -1):for j in range(i,n):if i==j:dp[i][j] = nums[i]else:if i+3<=j:dp[i][j] = max(dp[i][i]+dp[i+2][j], dp[i+1][i+1]+dp[i+3][j])elif i+2<=j:dp[i][j] = max(dp[i][i]+dp[i+2][j], dp[i+1][i+1])else:dp[i][j] = max(dp[i][i], dp[i+1][i+1])return dp[0][n-1]

动态规划+滚动数组
0-----------------n
设f(n)为到当前家的最大收益，如果我偷取了第n家，则当前收益为nums[n]+f(n-2)
如果不偷第n家，那么当前的收益为f(n-1)
f(n) = max(nums[n]+f(n-2), f(n-1))
边界条件为:
f(0) = nums[0]
f(1) = max(nums[0],nums[1])
循环推导下去：
f(2) = max(nums[2]+f(0),f(1))
f(3) = max(nums[3]+f(1),f(2))
通过滚动数组可以在不增加空间复杂度的情况下完成计算

class Solution:def rob(self, nums: List[int]) -> int:length = len(nums)if length==0:return 0if length==1:return nums[0]m = nums[0]n = max(nums[0], nums[1])for i in range(2, length):t = max(m+nums[i], n)m = n n = treturn n

343. 整数拆分（中等）

动态规划的适用于在计算当前结果的同时，可以利用到前一个步骤中计算的结果。
相当于当前最优结果可能是由子集中最优结果组合而成的。

class Solution:def integerBreak(self, n: int) -> int:dp = [0] * (n+1)for i in range(2, n+1):for j in range(i):dp[i] = max(dp[i], j*(i-j), j*dp[i-j])return dp[n]

位运算

67. 二进制求和

运算过程：
a = 0000 1111, b = 0000 0010
a ^ b      = 0000 1101         --> 新的a
(a&b) << 1 = 0000 0100         --> 新的ba ^ b      = 0000 1001         --> 新的a
(a&b) << 1 = 0000 1000         --> 新的ba ^ b      = 0000 0001         --> 新的a
(a&b) << 1 = 0001 0000         --> 新的ba ^ b      = 0001 0001         --> 答案是：10001
(a&b) << 1 = 0000 0000         --> b已经为：0000 0000

class Solution:def addBinary(self, a, b) -> str:x, y = int(a, 2), int(b, 2)while y:answer = x ^ ycarry = (x & y) << 1x, y = answer, carryreturn bin(x)[2:]

137. 只出现一次的数字（1） middle

187. 重复的DNA序列 middle

191. 位1的个数

260. 只出现一次的数字（2） middle

318. 最大单词长度乘积 middle

421. 数组中两个数的最大异或值 middle

数学、矩阵

50. pow(x,n) middle

暴力解法直接n个x相乘，时间复杂度为O(n)
快速幂算法：O(log n)时间复杂度的分治算法

class Solution:def myPow(self, x: float, n: int) -> float:if (x==0):return 0if (n==0):return 1if n<0:return 1/self.myPowHelper(x, -n)else:return self.myPowHelper(x, n)def myPowHelper(self, x, n):if n==1:return xif(n%2==0):res = self.myPowHelper(x,n//2)return res*reselse:res = self.myPowHelper(x,n//2)return res*res*x

70. 爬楼梯

118. 杨辉三角 |

# 给定一层的列表，建立子函数，求解下一层的杨辉三角
# 标定第一层和第二层的特殊值，检查numRows，直接赋值
class Solution:def generate(self, numRows: int) -> List[List[int]]:ans = []if numRows>=1:ans.append([1])if numRows>=2:ans.append([1,1])def g(n):nu = []for i in range(0,len(n)-1):nu.append(n[i]+n[i+1])return [1] + nu + [1]n = [1,1]for i in range(2,numRows):n = g(n)ans.append(n)return ans# 优化，不循环调用子函数，而是建立层数循环，去ans中查值
# 可以充分利用杨辉三角的对称性减少计算
class Solution:def generate(self, numRows: int) -> List[List[int]]:ans = []for i in range(0, numRows):n = [None for _ in range(i+1)]for j in range(i+1):#  1 4 6 4 1# j = 1  j=3  i = 4if j==0 or j==i:n[j] = 1else:n[j] = ans[i-1][j-1] + ans[i-1][j]ans.append(n)return ans

119. 杨辉三角 ||

方法：

数学二项式解题
根据上一行的列表，生成当前行列表

# 方法一
class Solution:def getRow(self, rowIndex: int) -> List[int]:res = [1]for i in range(1, rowIndex + 1):res.append(int(res[i - 1] * (rowIndex - i + 1) / i))return res# 方法二
class Solution:def getRow(self, rowIndex: int) -> List[int]:def getk(n):ans = []for i in range(1,len(n)):ans.append(n[i]+n[i-1])return [1]+ans+[1]if rowIndex==0:return [1]n = []for i in range(rowIndex):print(n)n = getk(n)return n

168. Excel表列名称

通过【除留余数法】将数字 n 由 10 进制转换为 26 进制

# 依次储存n除以26的余数，例如：
# 1000%26 = 12    1000//26 % 26=12  1000//26//26%12 = 1
# 所以1000对应的列名称为ALL
# 0的处理上比较困难
# 当n=26， ret=1，pos=0，则对应元素A0，但实际对应为Z
# 当n=26-1，ret=0，pos=25,则对应元素为Z（将A对应为0,即Z=25+65  A=0+65）
class Solution:def convertToTitle(self, n: int) -> str:ans = []while n>0:n= n - 1ans.insert(0,n%26)n = n//26return "".join(chr(i+65) for i in ans)

171. Excel表列序号

基础的26进制转10进制：

# 从后往前遍历，用count记录位数
// A code block
var foo = 'bar';
# 从前往后遍历，每次读入新元素，ans直接进位
class Solution:def titleToNumber(self, s: str) -> int:num = 0for i in s:num = num*26 + (ord(i)-64)return num

172. 阶乘后的零

方法：

计算阶乘，并通过取余、右移查询0的个数（两个大数字相乘的流行方法它的成本是O(log x * log y)）
计算因子5。阶乘后元素尾部的0取决于阶乘中10的个数，即5*2的个数。根据阶乘，至少每2个元素就存在一个2（2,4,6,8……），至少5个元素存在一个5（5,10,15,20,25……），所以最终阶乘后0的个数取决于因子5的数目，而因子5存在于间隔为5的元素中。

# 方法一
class Solution:def trailingZeroes(self, n: int) -> int:sum = 1for i in range(2, n+1):sum *= izero_count = 0while sum%10 == 0:zero_count += 1sum = sum//10return zero_count
# 方法二
class Solution:def trailingZeroes(self, n: int) -> int:count = 0for i in range(5,n+1,5):while i%5==0:count += 1i = i//5return count

1232. 缀点成线

直线的表示方式有两种：

一般式：Ax+By+C=0（AB≠0）。为方便后续计算，将所有点向 (-P0x, -P0y)方向平移，即将P0移到原点，则根据两点确定一条直线，P0和P1构成了一条穿过原点的直线，只需要检查其他点是否在该直线上。
两点式，如果直线过定点(x1,y1) (x2,y2)，则对于直线上的点(x,y)满足(y-y1)/(x-x1)=(y-y2)/(x-x2)，为了避免(x-x1)、(x-x2)为零，将除法转换为乘法，选择P0、P1为定点。

# 方法一
class Solution:def checkStraightLine(self, coordinates: List[List[int]]) -> bool:n = len(coordinates)for i in range(1,n):coordinates[i][0] = coordinates[i][0] - coordinates[0][0]coordinates[i][1] = coordinates[i][1] - coordinates[0][1]# Ax+BY=0  ---->y = kxA = coordinates[1][1]B = -coordinates[1][0]for i in range(2,n):if A*coordinates[i][0] + B*coordinates[i][1]!=0:return False        return True
# 方法二
class Solution:def checkStraightLine(self, coordinates: List[List[int]]) -> bool:for i in range(2, len(coordinates)):if (coordinates[i][1]-coordinates[0][1])*(coordinates[1][0]-coordinates[0][0]) != (coordinates[i][0]-coordinates[0][0])*(coordinates[1][1]- coordinates[0][1]):return Falsereturn True

图论

遍历：深度优先遍历、广度优先遍历、并查集

399. 除法求值 middle

from collections import defaultdictclass Solution:def calcEquation(self, equations: List[List[str]], values: List[float], queries: List[List[str]]) -> List[float]:#创建结果listfinal_result = []#先创建图self.graph = defaultdict(dict)for (x,y),val in zip(equations,values):self.graph[x][y] = valself.graph[y][x] = 1/val# DFS# for i in queries:#     start, end = i[0], i[1]#     visited = set()#     final_result.append(self.dfs(start, end, visited))# BFS 广度优先的难度就在于如何计算start与每个位置的值,从任一起点，遍历所有该起点能达到的位置，并计算权重更新有向图print(self.graph)for i in self.graph:visited = set()queue = [i]weight = [1]while queue:node = queue.pop() # list.pop()返回list的第一个元素w = weight.pop()  # 从i到当前pop结点的权重  visited.add(node)length = len(self.graph[node])for j in self.graph[node]:if j not in visited:visited.add(j)queue.append(j)self.graph[i][j] = w*self.graph[node][j]weight.append(self.graph[i][j])for i in queries:start, end = i[0], i[1]if start in self.graph:if start == end:final_result.append(1)elif end in self.graph[start]:final_result.append(self.graph[start][end])else:final_result.append(-1)else:final_result.append(-1)return final_resultdef dfs(self, start, end, visited):if start not in self.graph:  # 如果图中不存在以start为起点，则直接返回-1return -1if start == end:    return 1  # 如果终点和起点在一个位置，则直接返回1visited.add(start)# 否则按DFS策略，遍历与start相邻的每个结点，因为如果a->b，那么存在有向边b->a，则无法求解，所以使用visited保存每个被访问过的结点，避免重复访问。for i in self.graph[start]:if i == end:return self.graph[start][i]elif i not in visited:visited.add(i)v = self.dfs(i, end, visited)if v != -1:return self.graph[start][i] * vreturn -1

547. 省份数量

class Solution:def findCircleNum(self, isConnected: List[List[int]]) -> int:city = len(isConnected)total = cityparent = {}for i in range(city):if i not in parent:parent[i] = Nonedef find(index):while parent[index] != None:index = parent[index]return indexdef union(index1, index2):m = find(index1)n = find(index2)if m != n:parent[m] = nfor i in range(city):for j in range(i+1, city):if isConnected[i][j]:union(i,j)total = total - 1# 可以查看根节点为None的city数目，标识了省份；也可以记录初始连通数目，每次执行合并，数目减一num = sum([parent[i]==None for i in range(city)]) return total

684. 冗余连接 middle

方法：

并查集可以解决连通域问题，当union两个元素时，发现已经属于同一个根节点，则对应两元素的边为冗余连接。
DFS或者BFS，首先建图，当遍历的点被访问过，则连接两元素的边属于冗余连接。

并查集在建立parents时，通常选择两种，一种是均为None，最终parents为None的结点表示根节点；另一种是[0,1,2,3,4]与下标和结点对应，满足index = parents[index]的节点为根节点。

在本题中结点为1,2,3，…，N，在读入时人为地为结点减一，变为0,1，2，…,N，与parents中[0,1,2,…]对齐，在输出时将结点序号修正。

# 并查集 DFS BFS都可以，并查集可以处理连通分量问题，更简单
# DFS BFS需要根据给定edges建图
from collections import defaultdict
class Solution:def findRedundantConnection(self, edges: List[List[int]]) -> List[int]:# 建图# graph = defaultdict(set)# for i in edges:#     (m,n) = i#     graph[m].add(n)#     graph[n].add(m)ans = [] # 存储二维数组中最后出现的边length = set()for i in edges:(m,n) = ilength.add(m)length.add(n)parents = [i for i in range(len(length))]def find(index):while index != parents[index]:index = parents[index]return indexdef union(index1, index2):mm = find(index1)nn = find(index2)if mm!=nn:parents[mm] = nnelse:ans[:] = [index1+1, index2+1]  # 每次合并重复，即出现重复冗余连接for i in edges:union(i[0]-1, i[1]-1)return ans

上一种方法执行时间较长并且在序号对齐过程中，容易出错。使用None，则会避免序号对齐的麻烦，只需要将parents长度置为length+1，对[1:length]进行操作。

from collections import defaultdict
class Solution:def findRedundantConnection(self, edges: List[List[int]]) -> List[int]:ans = [] # 存储二维数组中最后出现的边length = set()for i in edges:(m,n) = ilength.add(m)length.add(n)parents = [None for _ in range(len(length)+1)]def find(index):while None != parents[index]:index = parents[index]return indexdef union(index1, index2):mm = find(index1)nn = find(index2)if mm!=nn:parents[mm] = nnelse:ans[:] = [index1, index2]  # 每次合并重复，即出现重复冗余连接for i in edges:union(i[0], i[1])return ans

721. 账户合并

class DSU:def __init__(self):self.p = range(10001)def find(self, x):if self.p[x] != x:self.p[x] = self.find(self.p[x])return self.p[x]def union(self, x, y):self.p[self.find(x)] = self.find(y)class Solution(object):def accountsMerge(self, accounts):dsu = DSU()em_to_name = {}em_to_id = {}i = 0for acc in accounts:name = acc[0]for email in acc[1:]:em_to_name[email] = nameif email not in em_to_id:em_to_id[email] = ii += 1dsu.union(em_to_id[acc[1]], em_to_id[email])ans = collections.defaultdict(list)for email in em_to_name:ans[dsu.find(em_to_id[email])].append(email)return [[em_to_name[v[0]]] + sorted(v) for v in ans.values()]

947. 移除最多的同行或同列石头

题目含义是：如果想移除一个石头，那么它所在的行或者列必须有其他石头存在。我们能移除的最多石头数是多少？也就是说，只有一个石头在连通分量中，才能被移除。对于连通分量而言，最理想的状态是只剩一块石头。对于任何容量为n一个连通分量，可以移除的石头数都为n-1。

一定可以把一个连通图里的所有顶点根据这个规则删到只剩下一个顶点；故最多可以移除的石头的个数 = 所有石头的个数 – 连通分量的个数。

# 并查集
from collections import defaultdict
class Solution:def removeStones(self, stones: List[List[int]]) -> int:dict_x = defaultdict(set)dict_y = defaultdict(set)for i in range(len(stones)):x,y = stones[i]dict_x[x].add(i)dict_y[y].add(i)def find(index):while parents[index]!=None:index = parents[index]return indexdef union(index1, index2):m = find(index1)n = find(index2)if m!=n:parents[m] = nn = len(stones)parents = [None for _ in range(n)]for i in range(n):x,y = stones[i]for j in dict_x[x]:union(i,j)for k in dict_y[y]:union(i,k)            h = 0for i in parents:if i==None:h = h+1return n-h# 深度优先搜索
class Solution:def removeStones(self, stones: List[List[int]]) -> int:dict_X = collections.defaultdict(list)dict_Y = collections.defaultdict(list)for x, y in stones:dict_X[x].append((x, y))dict_Y[y].append((x, y))visited = set()def dfs(node):if node in visited:returnvisited.add(node)x, y = nodefor i in dict_X[x]:dfs(i)for i in dict_Y[y]:dfs(i)ans = 0for i in stones:i = tuple(i)if i not in visited:ans += 1dfs(i)return len(stones) - ans

1202. 交换字符串的元素 middle

# 任意多次交换，建图，通过DFS或者BFS遍历图，建立连通分量
class Solution:def smallestStringWithSwaps(self, s: str, pairs: List[List[int]]) -> str:from collections import defaultdictlength = len(s)ans = [0]*lengthgraph = defaultdict(set)for (i,j) in pairs:graph[i].add(j)graph[j].add(i)def dfs(node, visited, ret):for i in graph[node]:if i not in visited:visited.add(i)ret.add(i)dfs(i, visited, ret)visited = set()for i in range(len(s)):ret = set()if i not in visited:visited.add(i)ret.add(i)dfs(i, visited, ret)ret_index = sorted(ret)str_index = sorted([s[j] for j in ret_index])for h,l in zip(ret_index, str_index):ans[h] = lreturn ''.join(ans)

1631. 最小体力消耗路径

# 二分查找+dfs或者bfs
class Solution:def minimumEffortPath(self, heights: List[List[int]]) -> int:m, n = len(heights), len(heights[0])left, right, ans = 0, 10**6 - 1, 0while left <= right:mid = (left + right) // 2q = collections.deque([(0, 0)])seen = {(0, 0)}while q:x, y = q.popleft()for nx, ny in [(x - 1, y), (x + 1, y), (x, y - 1), (x, y + 1)]:if 0 <= nx < m and 0 <= ny < n and (nx, ny) not in seen and abs(heights[x][y] - heights[nx][ny]) <= mid:q.append((nx, ny))seen.add((nx, ny))if (m - 1, n - 1) in seen:ans = midright = mid - 1else:left = mid + 1return ans

最小生成树

1584. 连接所有点的最小费用

Kruskal 算法和Prim 算法是解决最小生成树问题的经典方法。

Kruskal算法在每次迭代中选择不在同一个连通分量的最短边，并合为相同连通分量，则可以很容易的用并查集方法解决。在并查集的处理状态，每个顶点自成一个连通分量。对图中的边排序，依次查找当前最短的边l，如果该边不在同一个连通分量，则连接对应顶点，则最小代价+l；直到找到与顶点数目-1条边，构成最小生成树。

class Solution:def minCostConnectPoints(self, points: List[List[int]]) -> int:def dis(point1, point2):return abs(point1[0]-point2[0])+abs(point1[1]-point2[1])class findunion:def __init__(self, n):self.parents = [i for i in range(n)]def find(self, index):while index != self.parents[index]:index = self.parents[index]return indexdef union(self, index1, index2):m = self.find(index1)n = self.find(index2)if m==n:return Falseelse:self.parents[m]=nreturn Trueret = 0num = 1 # n个顶点有n-1条边edge = []length = len(points)if length<=1:return 0fd = findunion(length)for i in range(length):for j in range(i+1, length):edge.append([dis(points[i],points[j]),i,j])def takedist(elem):return elem[0]edge.sort(key = takedist)   # 对距离进行排序, key，具体的函数的参数就是取自于可迭代对象中，指定可迭代对象中的一个元素来进行排序。# prim和kruskal的差别在这里出现，kruskal从整个边序列中找最短边，prim找当前S中的最小边for dist, m, n in edge:if fd.union(m,n):  # 如果返回True，则不在同一个连通分量中ret += distnum += 1if num==length:return ret

简单-中等题

概率论

哈希

169. 多数元素

双指针

26. 删除排序数组中的重复项

27. 移除元素

28. 实现 strStr()

38. 外观数列

58. 最后一个单词的长度

89. 合并两个有序数组

125. 验证回文串

141. 环形链表

167. 两数之和 ||

228. 汇总区间

查找及插入问题

二分查找及其变种

33. 搜索旋转排序数组

35. 搜索插入位置

69. x的平方根

153. 寻找旋转排序数组中的最小值

704. 二分查找

852. 山脉数组的峰顶索引

队列、栈

155. 最小栈

895. 最大概率栈 （Hard）

单调栈

42. 蓄水池

84. 柱状图中的最大矩形

496. 下一个更大元素|

738. 每日温度

901. 股票价格跨度

数组

66. 加一

67. 二进制求和

189. 旋转数组 middle

560. 和为k的子数组

674. 最长连续递增序列

链表

19. 删除链表的倒数第N个结点

83. 删除排序链表中的重复元素(hash)

138. 复制带随机指针的链表

141. 环形链表

160. 相交链表

203. 移除链表元素

树

100. 相同的树（递归）

101. 对称二叉树

104. 二叉树的最大深度

107. 二叉树的层序遍历 ||

108. 将有序数组转换为二叉搜索树（递归）

110. 平衡二叉树

111. 二叉树的最小深度

112. 路径总和

动态规划

53. 最大子序和

70. 爬楼梯

121. 买卖股票的最佳时机 |

122. 买卖股票的最佳时机 ||

198. 打家劫舍

343. 整数拆分（中等）

位运算

67. 二进制求和

137. 只出现一次的数字（1） middle

187. 重复的DNA序列 middle

191. 位1的个数

260. 只出现一次的数字（2） middle

318. 最大单词长度乘积 middle

421. 数组中两个数的最大异或值 middle

数学、矩阵

50. pow(x,n) middle

70. 爬楼梯

118. 杨辉三角 |

119. 杨辉三角 ||

168. Excel表列名称

171. Excel表列序号

172. 阶乘后的零

1232. 缀点成线

图论

遍历：深度优先遍历、广度优先遍历、并查集

895. 最大概率栈（Hard）