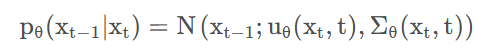1. 到目前为止，有3种类型的生成模型，即GAN、VAE和基于Flow的模型。它们在生成高质量样本方面获得了巨大的成功，但每一种都有其自身的一些局限性。例如，GAN模型由于其对抗性训练的性质，以潜在的不稳定的训练和较少的生成多样性而闻名。VAE依赖于代用损失。基于Flow的模型必须使用专门的架构来构建可逆变换。
2. 扩散模型(Diffusion Models)是受非平衡热力学(Non-equilibrium thermodynamics )的启发。它们定义了一个扩散步骤的马尔可夫链(Markov chain)，以缓慢地向数据添加随机噪声，然后学习逆转扩散过程(learn to reverse the diffusion process)，从噪声中构建所需的数据样本。与VAE或基于Flow的模型不同的是，扩散模型是以固定的程序学习的，潜在的变量具有高维度（与原始数据相同）。
What are Diffusion Models?
1. 一些基于扩散的生成模型被提出，其下有类似的想法，包括扩散概率模型（diffusion probabilistic models，Sohl-Dickstein et al.，2015）、噪声条件下的得分网络（noise-conditioned score network, NCSN, Yang & Ermon，2019），以及去噪扩散概率模型（denoising diffusion probabilistic models, DDPM, Ho等，2020）.
-
Forward diffusion process(前向扩散过程)
-
给出一个从真实数据分布中采样的数据点
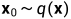, 让我们定义一个前向扩散过程(Forward diffusion process)，在这个过程中，我们以T个步骤向样本添加少量高斯噪声，产生一连串的噪声样本
.步长是由一个方差表控制
.
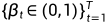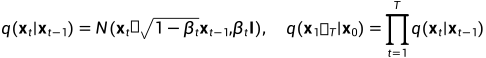
随着步长t的增大，数据样本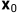
逐渐失去了其可辨识的特征。最终当
，
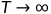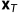相当于一个各向同性的高斯分布(isotropic Gaussian distribution)。
上述过程的一个很好的特性是，我们可以用重参数化技巧(reparameterization trick)在任何任意时间步长t的封闭形式下对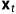
进行采样。令
，
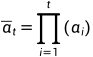
备注（本人推导）：
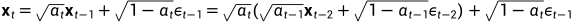
因为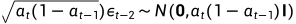
, 
,
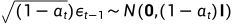所以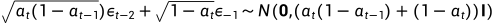
.
又因为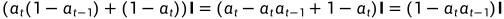
,
所以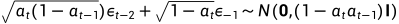
所以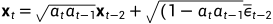
，以此类推，
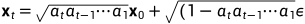. 因为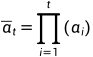
所以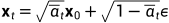
通常情况下，当样本变得更加嘈杂时，我们可以承受更大的更新步骤，因此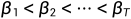
，从而可以得到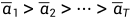
-
Connection with stochastic gradient Langevin dynamics(与随机梯度朗之万动力学的联系)
郎之万动力学是一个来自物理学的概念，为统计学上的分子系统建模而开发。与随机梯度下降相结合，随机梯度朗之万动力学(stochastic gradient Langevin dynamics)（Welling & Teh 2011）可以从概率密度p(x)中产生样本，在马尔科夫链的更新中只使用梯度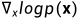
:
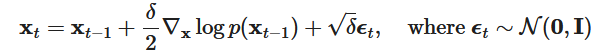
其中，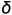
是步长大小. 当，
，
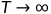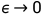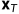等于真实概率密度p(x).
与标准SGD相比，随机梯度Langevin动力学将高斯噪声注入到参数更新中，以避免塌陷到局部最小值。
-
Reverse diffusion process(反向扩散过程)
如果我们能将上述过程倒过来，从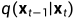
中取样，我们就能从高斯噪声输入中重现出真实的样本,
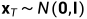. 注意到如果
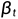足够小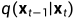，也将是高斯. 不幸的是，我们难以轻易估计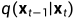，因为它需要使用整个数据集，因此我们需要学习一个模型
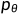来近似这些条件概率，以便运行反向扩散过程。
扩散过程是将原始数据不断加噪得到高斯噪声，逆扩散过程是从高斯噪声中恢复原始数据，我们假定逆扩散过程仍然是一个马尔可夫链的过程，要做的是 X T − > X 0，用公式表达如下：
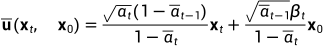（1）
逆扩散过程模型不应当事先知道x0，故需要将x0用xt代替：
因为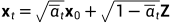
，所以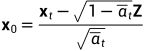
带入式（1）
因此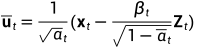 
-
优化目标函数
4.1损失函数公式推导
得到损失函数如下：
这里论文将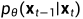
分布的方差设置成一个与
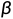相关的常数，因此可训练的参数只存在于其均值中。对于两个单一变量的高斯分布p和q而言，它们的KL散度为:
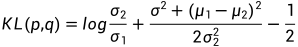
备注：信息熵的计算公式如下：
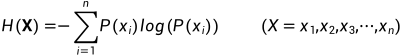
对于0-1分布的问题，由于其结果只用两种情况，是或不是，设某一件事情发生的概率为 P(x)，则另一件事情发生的概率为 1−P(x)，所以对于0-1分布的问题，计算熵的公式可以简化如下：
4.1.1 相对熵（KL散度）
如果对于同一个随机变量X有两个单独的概率分布P(x) 和 Q(x)，则我们可以使用KL散度来衡量这两个概率分布（样本的真实分布P(X)和模型所预测的分布Q(X)）之间的差异：
KL散度越小，表示P(X)与Q(X)的分布更加接近，可以通过反复训练Q(X)来使Q(X)的分布逼近P(X)。
4.1.2 交叉熵
首先将KL散度公式拆开：
前者H(P(X))表示信息熵，后者为交叉熵，因此KL散度 = 交叉熵 – 信息熵.
交叉熵公式表示为：
在机器学习训练网络时，输入数据与标签常常已经确定，那么真实概率分布 P(X) 也就确定下来了，所以信息熵在这里就是一个常量。由于KL散度的值表示真实概率分布 P(X) 与预测概率分布 Q(X) 之间的差异，值越小表示预测的结果越好，所以需要最小化KL散度，而交叉熵等于KL散度加上一个常量（信息熵），且公式相比KL散度更加容易计算，所以在机器学习中常常使用交叉熵损失函数来计算loss就行了。
-
交叉熵能够衡量同一个随机变量中的两个不同概率分布的差异程度，在机器学习中就表示为真实概率分布与预测概率分布之间的差异。交叉熵的值越小，模型预测效果就越好。
-
交叉熵在分类问题中常常与softmax是标配，softmax将输出的结果进行处理，使其多个分类的预测值和为1，再通过交叉熵来计算损失。
4.2 损失函数代码实现
-
算法流程
5.1损失函数公式推导
https://lilianweng.github.io/posts/2021-07-11-diffusion-models/