女士们，先生们：还在人类智慧发展的最初阶段，人们就已经明确地把空间和时间看做发生各种事件的舞台。这种概念一代一代地传下来，没有什么实质性的改变；并且，从精密科学开始发展以来，它就被用作对宇宙进行数学描述的基础。伟大的牛顿①大概是第一个清楚地阐明了古典的时空概念的人，他在他的《原理》一书中写道：
>>>>
绝对空间就其本质而言，是不依赖于任何外界事物的，它永远是相同的，不变的。绝对的、真实的数学时间，就其自身及其本质而言，是永远均匀地流动的，不依赖于任何外界事物。
过去，人们极其坚定地相信这些古典的时空概念是绝对正确的，因此，哲学家们常常把它们看做某种先验的东西，而科学家们连想也没有想到可能有人对这些概念产生怀疑。
但是，在20 世纪刚开始的时候，人们开始了解到，要是硬把实验物理学最精密的方法所得到的许多结果纳入古典时空概念的框框，就会出现一些显而易见的矛盾。这个事实使当代最出色的物理学家爱因斯坦产生了一个革命的想法，他认为，如果抛开那些传统的借口，就根本没有任何理由把古典的时空概念看做绝对真理，人们不仅有可能、并且也应该改变这些概念，使它们同新的、更精密的实验相适应。事实上，既然古典的时空概念是在人类日常生活体验的基础上建立起来的，那么，要是今天根据高度发展的实验技术建立的精密的观察方法表明，那些旧的概念过于粗糙，过于不精确，它们之所以能够用在日常生活中，能够用于物理学发展的初期，仅仅是由于它们同正确概念的差异相当微小，那么，我们就不应该大惊小怪了。同样，要是现代科学所探索的领域不断扩展，把我们带到两者的差异变得非常巨大、以致古典概念根本无法应用的场合，我们也不应该感到惊讶。
使古典概念从根本上遭到批判的一个最重要的实验结果，是人们发现了真空中的光速是一个常数（等于300 000 公里每秒），并且是一切可能的物理速度的上限。这个出人意料之外的重要结论，主要是从美国物理学家迈克耳孙和莫利②的实验得出的。19 世纪末，他们千方百计想观察地球的运动对光的传播速度的影响。他们的脑子里还是当时流行的观点，认为光是一种在被称为“以太”的媒质中运动的波。这样，它的表现就应该像在池塘表面上运动的水波那样。当时人们还认为，地球也是在穿过这种以太媒质运动的，很像是一艘在水面上运动的小船。在小船上的乘客看来，小船激起的涟漪朝着小船运动方向向前扩展的速度，要比涟漪向后扩展的速度慢一些，因为在前一种情况下要从涟漪原来的速度减去小船的速度，而在后一种情况下却要把两个速度相加起来。我们把这叫做速度相加定理，这个定理一直被看做是不证自明的。因此，在穿过以太运动时，光的速度同样应该随着它相对于地球运动的方向的不同而显得不尽相同。既然如此，只要测量出光在不同方向上的速度，就应该能够测定地球在以太中的运动速度了。
但是，迈克耳孙和莫利却发现，地球的运动对光速根本没有任何影响，不管在哪一个方向上，光的速度都是完全相等的。这个发现使他们本人和整个科学界都大吃一惊。这个奇怪的结果使他们产生了一种想法：也许是非常不巧，在他们进行那个实验的时候，地球在其环绕太阳运动的轨道上正好处在相对于以太静止不动的状态。为了检验事情是不是这样，过了6 个月，也就是当地球在太阳的另一侧朝着相反的方向运行时，他们又重复做了那个实验。但是，这一次也同样测不出光速有任何不同。
既然已经确定，光速的表现同水波的速度不一样，那么，剩下来的可能性就是假定它的表现和子弹相同了。如果我们用小船上的枪射出一颗子弹，那么，在乘客看来，这颗子弹不管是朝哪个方向射出，它离开运动中的小船的速度都是相同的——事实上，迈克耳孙和莫利也已经发现，从运动中的地球朝不同方向发射出的光，它们离开地球的速度也全都相等。但是在这种情况下，站在岸上的观察者就会发现，朝着小船前进方向射出的子弹的运动速度，要比朝着相反方向射出的子弹更快一些：在前一种情况下，小船的速度会同子弹的出膛速度相加在一起，而在后一种情况下，却要从子弹的出膛速度减去小船的速度——而这同样是速度相加定理告诉我们的。与此相应，我们也应该认为，从某个相对于我们与运动的光源发射出的光，它的速度必定会随着同运动方向所形成的发射角的不同而不同。
但是，实验告诉我们，实际情形也不是如此。我们就拿电中性的 π 介子作为例子吧！π 介子是一种非常小的亚原子粒子，它在衰变时会发射出两个光脉冲。已经发现，不管这两个脉冲的发射方向同原来母 π 介子的运动方向有什么关系，它们射出的速度总是相同的，甚至在 π 介子本身以接近于光速的速度运动时也是这样。
于是我们发现，前面提到的两种实验都没有得到预期的结果：前一种实验表明，光速的表现同常规水波的速度不一样；而后一种实验则表明，光速的表现也不同于常规子弹的速度。
总而言之，我们的发现是：不管观察者在做什么运动（我们是从运动中的地球上进行观察的），也不管光源在做什么运动（我们所观察的是从运动中的 π 介子发出的光），光在真空中的速度总是具有恒定的值。
我前面提到过，光速有另外一个性质——光速是无法超越的极限速度。这又是怎么回事呢？
“啊，”你们可能会说，“难道不可能把若干个比较小的速度相加起来，构成一个超过光速的速度吗？”
举个例子吧！我们可以设想有一列跑得非常快的火车，就说它的速度等于光速的3/4 吧，再设想有一个人在车顶上朝火车头跑去，他的速度也等于光速的3/4。
按照速度相加定理，这两个速度合成的总速度应该等于光速的1.5 倍，因此，那个在车顶上跑的人应该能够赶上并超过路边信号灯所发出的光束。但是，实际情况是：既然光速固定不变是一个实验事实，所以，在现在所说的这个例子里，合成速度就必定小于我们上面所预期的速度值——它不能超过极限值c。因此，我们应该得出结论说，即使对于比较小的速度来说，古典的速度相加定理也肯定是不正确的。
关于这个问题的数学处理，我不想在这里细说，但是我可以告诉你们，在计算两个叠加运动的合成速度方面，它得到了一个非常简单的新公式。
如果v1和v2是那两个要相加的速度，c 是光速，那么，合成速度与原来速度的关系应该是
从这个公式可以看出，如果原来两个速度都很小——我说很小，是同光速比较而言的——那么，上式分母的第二项同（1）相比较，就可以略去不计，这时，你所得到的就是古典的速度相加定理。但是，如果v1和v2都不算小，那么，你所得到的结果就总是比这两个速度的算术和小一些。例如，在上面所说的那个人在火车顶上奔跑的场合下，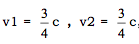
，这时，用上面公式得出的合成速度，
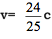，这仍然小于光的速度。
在一种特殊的场合下，即当原来两个速度当中有一个等于c 的时候，不管另一个速度有多大，用公式（1）所得出的合成速度都等于c。由此可见。不管把多少个速度相加起来，也永远得不到比光速更大的速度。
你大概也乐意知道，这个公式已经由实验加以证明了——人们在实验中确实发现，两个速度的合成值总是小于它们的和。
既然我们承认速度有一个上限，我们现在就可以着手批判古典的时空概念了。在这里，我们的第一支箭要对准根据这种概念建立起来的同时性概念。
“你把火腿炒鸡蛋端上你在伦敦的餐桌，正好与开普敦③矿井中那些炸药的爆炸同时。”——当你说这句话的时候，你一定认为，你知道你的意思是什么。但是，我马上就要指出，你并不知道你自己在说什么，并且严格他说，这句话是没有任何确切含意的。事实上，你有什么方法可以检验这两个事件到底是不是同时发生在两个不同的地方呢？你会说，只要在发生这两件事时，那两个地方的时钟指着同一个时刻就行了。但是，这时马上产生了一个问题：你怎样把这两个离得很远的时钟弄到一块，让它们同时指着同一个时刻呢？这样一来，我们就又回到原先的问题上来了。
由于真空中的光速不依赖于光源的运动状态和测量光速的系统，这件事是一个最精确地确定了的实验事实，我们就必须认为，下面所要介绍的测量距离和核对不同观察站的时钟的方法，是最为正当的方法，并且，要是你稍稍多想一想，你就一定会同意说，它同时也是唯一合理的方法。
设想我们从A 站发出一个光信号，让这个光信号一到达B 站，就马上返回A 站。这样，在A 站记录到的从发出信号到信号返回A 站的时间的一半，乘上固定不变的光速，应该就是A 站与B 站的距离。
如果在信号到达B 站的瞬时，当地的时钟正好指着A 站在发出信号和收到信号的瞬时所记录下的两个时间的平均值，我们就说，A 站和B 站的时钟是彼此对准了的。对固定在一个刚体上的各个观察站，用这种方法把时钟一一对准，我们最后就得到了我们所希望有的参考系，因而就能够回答两个在不同地点发生的事件是否同时的问题了。
但是，这些结果会不会为另一个参考系中的观察者所认可呢？为了回答这个问题，我们假定这两个参考系是固定在两个不同的刚体上的，或者就说是固定在两枚以同一固定不变的速度朝相反方向飞行的长火箭上吧。现在我们来看看，这两个参考系的时间怎样才能彼此对准。
假定每一枚火箭的头尾两端各有一个固定不动的观察者，这4 个观察者首先必须把他们的表彼此对准。这时，每一枚火箭上的两个人，都可以把前面所说对准时钟的办法变通一下，把他们的表彼此对准。这就是从火箭的正当中（这可以用量尺测量好）发出一个光信号，当这个信号从火箭的正当中传到它的头尾两端时，每一端的观察者就都把自己的表拨到零点。这样，按照前面的规定，这两个观察者已经把他们自己那个参考系中的同时性标准确定下来，把他们的表“对准”了——当然啦，这是从他们自己的观点出发来说的。
现在他们决定看看他们火箭上的时间记录是不是同另一枚火箭上的记录相符。譬如说，当处在不同火箭上的两个观察者彼此擦身而过时，看看他们的表是不是指着同一个时刻？这可以用下面的方法来检验：他们在每一枚火箭的几何中点插上一根带电的导体，让两枚火箭互相掠过，且它们的中点彼此对准时，在两根带电导体之间跳过一个电火花，这样一来，光信号便同时从每一枚火箭的中点向两端传播，如图（a）所示。过了一会儿，火箭2 上面的观察者2A 和2B 所看到的情形表示在图（b）上。这时火箭1 已经相对于火箭2 运动开了，两个光束朝着前后两个方向、移动了相等的距离。但是请大家注意这时发生了什么事情。由于观察者1B 是朝着向他射过来的光束运动的（在观察者2A 和2B 看来，情形就是这样），所以在火箭1 上向后行进的光束已经到达观察者1B 的位置。按照2A 和2B 的看法，这是因为这个光束所需要走过的距离比较短。因此，观察者1B 便把他的表拨到零点，而其他人都还没有动作。在图（c）中，光束已经到达火箭2 的两端，这时观察者2A 和2B便同时把他们的表拨到零点。只有到图（d）的情况出现时，火箭1上向前传播的光束才到达观察者1A 的位置，使他觉得是该把自己的表拨到零点的时候了。这样一来，我们就可以知道，在火箭2 上的两位观察者看来，火箭1 上的那两位并没有对好他们的表——他们的表不会显示出相同的时间。
当然啦，我们也很容易表明，在火箭1 上面的观察者看来，火箭2 上也发生了同样的情形。按照他们的看法，“静止不动的”正是他们自己的火箭，而在进行运动的应该是火箭2。现在是观察者2B 在朝着射向他的光束前进，而2A 却对着光束倒退。因此，在观察者1A 和1B 看来，是2A 和2B 没有把他们的表对好，而他们自己却是把表对好了的。
其所以会出现这种看法上的差异，是因为当几个事件发生在分隔开的地方时，这两组观察者就必须先进行计算，然后才能决定这些被分隔开的事件是不是同时发生；他们必须扣除光信号从遥远的地方传到他们那里所花费的时间，并且坚定地认为相对于他们来说，来自任何方向的光的速度都是恒定不变的（只有当几个事件发生在同一个地方，也就是不需要进行计算时，才能对这些发生在那个地方的事件是否同时作出普遍认可的判断）。既然这两枚火箭的地位是完全平等的，所以，要解决这两组观察者之间的争论，就只能够说，这两组观察者的说法，从他们各自的角度看来都是正确的；而究竟哪一方是“绝对”正确的问题，则没有任何物理意义。
我怕我这番冗长的议论已经把大家弄得十分疲倦了，不过，要是你们很细心地从头听下来的话，就一定会明白，一旦采纳我们上面所说的时空测量方法，绝对同时的概念就不复存在了—— 在某个参考系中的同一时间但在不同地点发生的两个事件，在另一个参考系看来，将变成被一定时间间隔分隔开的两个事件。
这种说法乍一听来是极端反常的。但是，如果我说，你在火车上吃晚饭的时候，你的汤和点心都是在餐车上同一个地方，但却是在铁路上相距很远的两个地方吃下去的，那么，你是不是也会觉得反常呢？其实，关于你在火车上吃晚饭这个例子，也可以换一种说法，说成是，在某个参考系中的同一地点，但在不同时间发生的两个事件，在另一个参考系看来，将变成被一定空间间隔分隔开的两个事件。
把这种“正常”的说法同上面那种“荒谬”的说法比较一下，你就会看出，这两种说法是完全对称的，只要把“时间”和“空间”这两个词对换一下，就可以把其中的一种说法变成另一种说法。
爱因斯坦的整个观点就是：在古典物理学中，时间被看做某种完全不依赖于空间和运动的东西，它是“均匀地流动的，不依赖于任何外界事物”（牛顿语）；与此相反，在新的物理学中，空间和时间却是紧密地联系在一起的，它们只不过是发生一切可以观察到的事件的均匀“时空连续统”的两个不同截面。把这种四维的连续统分裂为三维的空间和一维的时间纯粹是一种任意的作法，这与进行观察时所用的参考系有关。
在一个参考系看来，在空间中由距离 l、在时间上由间隔t 分开的两个事件，从另一个参考系看来，分开它们的空间距离将变成l'，时间间隔则变成t'，因此，从某种意义上说，我们可以说是把空间变换成时间或者把时间变换成空间了。同样也不难看出，为什么在我们看来，把时间变换成空间（像在火车上吃晚饭那个例子）是很普通的概念，而从空间变换成时间（这会使同时性变成相对的）却似乎是极为反常了。问题在于，如果我们用“厘米” 来测量距离，那么，相应的时间单位就不应该是常用的“秒”，而应该是一种“合理的时间单位”，它等于光信号走过1 厘米距离所花的时间，即0.000 000 000 03 秒。
这样一来，在我们日常经验的范围内，从空间间隔变换成时间间隔所产生的结果实际上是观察不到的，这就似乎证明了时间是某种绝对独立的，不变的东西这种古典观点。
但是，在研究速度极高的运动，例如在研究放射性物质所发射出的电子的运动或电子在原子内部的运动时，由于这时在某一时间内走过的距离同用合理时间单位所表示的时间属于同一个数量级，我们就必定会碰到上面所讨论的那两种效应，这时，相对论就变得非常重要了。即使在速度比较小的区域内，例如在研究我们太阳系中行星的运动时，由于天文观测已经非常精密，也可以观察到这些相对论性效应。不过，想观察到它们，就必须测出
行星运动每年总共只有几分之一弧秒的变化。
我上面已经尽力为大家说明，对古典时空概念进行批判会导致一个结论，即空间间隔实际上可以变换成时间间隔，时间间隔也可以变换成空间间隔，这就是说，在从不同的运动系统测量同一个距离或时间时，会得到不相同的数量值。
对这个问题进行比较简单的数学分析，就可以得出一个明确的计算这些值的变化的公式，不过，我不想在这里多谈这个问题。我只想简单地说，这个公式告诉我们，任何一个长度为l0的物体，当它以速度v 相对于观察者运动时，它的长度（在运动方向上）都会缩短，缩短的数量取决于它的速度，也就是说，观察者所测量到的长度l 将变成
从这个公式可以看出，当v 非常接近于c 时，l 变得越来越小。这就是著名的相对论空间缩短（尺缩）效应。我得赶快补充一点说明，这里的l 指的是物体在其运动方向上的长度。它与运动方向成直角的尺寸是不会改变的。结果，物体在其运动方向上便变扁了。
与此相似，一个需要花时间t0的过程，在从一个作相对运动的参考系对它进行观察时，它所花的时间，将变得长一些，也就是
请大家注意，随着v 的增大，t 也同样增大。事实上，当v 接近于c 时，t 会变得非常大，以致所发生的过程几乎停滞下来了。这就是相对论的时间延长（钟慢）效应。正因为这样，人们就产生了一种想法，认为如果宇航员们以接近于光速的速度遨游太空，他们变老的过程就会变得非常之慢，以至于他们几乎不会变老——他们可以永远活下去！
我希望大家不要忘记，这两种效应是完全对称的，因此，当一列快速运动的火车上的旅客，正在奇怪为什么那站在月台上的人长得那么瘦、动得那么慢的时候，那站在月台上的旅客对于行驶着的火车上的人，也正好有完全相同的想法哩。
乍一看来，这可能叫人觉得有悖常理。确实，这个问题引出了一个所谓“双生子佯谬”，其内容是：有两个孪生兄弟，一个出外旅游，另一个留在家里。按照我前面说明的理论，他们每个人根据他们对另一个人的观察，以及关于光信号要花多长时间才能到达，他们通过计算，都认为自己的兄弟会老得慢一些。现在的问题是：当那个出门旅游的兄弟回到家里，两人可以面对面地进行比较时（这时的比较不需要再进行任何计算，因为他们已经又一次处在同一个地方了），他们会发现什么样的结果呢？要想解答这个问题，就必须认识到这两人的立足点是不同的。那个外出的兄弟要想回家，就必须经历加速的过程——先是把速度减慢到零，然后朝着相反的方向重新受到加速。同他那留在家里的兄弟不一样，他一直处在非匀速运动的状态中。只有留在家里的那一个才始终保持匀速运动的条件，因此，他会认为他的兄弟现在并不显得更年轻一些是毫无道理的。
在结束这篇演讲之前，我还想再指出一件事。你们也许会觉得奇怪：究竟是什么东西妨碍着我们把物体的速度加速到比光速更快呢？真的，你们可能会这样想，如果我施加给物体的力足够大，时间又足够长，使得它一直不停地加速下去，最后是必定能达到我希望达到的任何速度的。
按照一般的力学原理，物体的质量决定了使物体开始运动或使运动物体加快速度的难度。质量越大，使速度增大某一数量的难度也越大。
任何物体在任何条件下都不能超过光速这个事实，使我们可以直接作出结论说，当物体的速度接近于光速的时候，进一步加速所碰到的阻力——换句话说即物体的质量——必定会无限制地增大。数学分析得出了一个计算这种关系的公式，它同公式（2）和（3）非常相似。如果m0是速度非常小的时候的质量，那么，当速度等于v 时，质量m 将是
可见，当v 接近于c 时，进一步加速所碰到的阻力（即质量）就会变成无限大。因此，c 便成为极限速度了。
质量发生相对论性变化的效应。是很容易通过实验在高速运动粒子上观察到的。我们就拿电子作为例子吧！电子是原子内部的一种非常小的粒子，它们围绕着原子的中心核而运动。由于它们极轻，很容易对它们进行加速。当把电子从原子中取出并放到特制的粒子加速器中，使它们受到强大电力的作用时，可以把它们加速到非常非常高的速度，同光速只相差一个零点零零几的百分数。在这样大的速度下，进一步加速它们所受到的阻力，相当于比正常电子质量大40 000 倍的质量——这是已经在美国加利福尼亚州的斯坦福实验室中证明了的。
不仅如此，时间的延长也已经得到了证实。瑞士日内瓦郊外的欧洲核子研究中心（CERN）高能物理实验室已经发现，不稳定的 μ 子（一种基本粒子，在正常情况下会在百万分之一秒内发生放射性衰变）在一种形状像个大空心轮胎的圆环形机器中高速回旋运动时，它的寿命会延长30 倍。而这个倍数正好是根据前面的时间延长公式所得出的值。
可见，在这样大的速度下，古典力学已经完全不再适用了，这时，我们就进入了纯相对论的领域。
① 牛顿（Newton），1642~1727，英国物理学家和数学家，古典物理学的奠基者。他的《原理》一书的全名为《自然哲学的数学原理》。——译者注
② 迈克耳孙（Michelson），1852~1931；莫利（Morley），1838~1923。这里指的是他们利用他们发明的干涉仪所做的、否定了以太存在的实验。迈克耳孙因各种光学研究成果而获得1907 年诺贝尔物理学奖。——译者注
③ 开普敦，南非的一个地名，以盛产黄金著称。——译者注
（本文选自《物理世界奇遇记》（美）G.伽莫夫 （Gamow，G.），（英）斯坦纳德（Stannard，R.）著；吴伯泽译．）
∑编辑 | Gemini
来源 | 物理世界奇遇记
算法数学之美微信公众号欢迎赐稿
稿件涉及数学、物理、算法、计算机、编程等相关领域
经采用我们将奉上稿酬。
投稿邮箱：math_alg@163.com