
一、极大似然估计概述
极大似然估计是频率学派的进行参数估计的法宝,基于以下两种假设前提:
①某一事件发生是因为该事件发生概率最大。
②事件发生与模型参数θ有关,模型参数θ是一个定值。
极大似然估计是通过已知样本数据,来推导出最大概率出现这个事实的模型参数值,并将这一参数值作为估计的真实值。
举例:抛硬币10次,若出现一次结果为5次正面朝上,5次反面朝上。设出现这一结果与P有关,则似然函数为L(P)=p^5*(1-p)^5,对其取对数求导,令导数为零,求得p为0.5。则我们有理由认为当p等于0.5时,最有可能出现抛硬币10次,其中5次正面朝上,5次反面朝上这样的结果。
二、极大似然原理及思想
极大似然原理的直观想法是:一个随机试验如有若干个可能的结果A,B,C,…。若在一次试验中,结果A出现,则一般认为试验条件对A出现有利,也即A出现的概率很大。
极大似然原理:若事件A发生的概率与参数 θ有关,θ取值不同则 P(A)也不同。记事件A发生的概率为 P(A|θ). 若一次试验事件中,A发生了,可认为此时的 θ值是在其定义域内,使得P(A|θ) 达到最大的那一个。
极大似然估计是建立在极大似然原理基础上的一个统计方法。它是一种参数估计,在样本满足独立同分布情况下,通过已知的样本数据,来推导最大概率出现这个事实的模型参数值,若已知某个参数能使得这个样本出现的概率最大,就将这一参数值作为估计的真实值。即模型已知,参数未知,通过已知模型推导出参数最可能的值。
三、似然函数与概率密度函数:L(θ|x)= f(x|θ)
|
似然函数:L(θ|x) |
概率密度函数: f(x|θ) |
|
在给定一个样本X后,在不同θ下,推测这个样本出现的可能性多大 |
在给定参数θ情况下,样本X出现的可能性多大 |
似然函数与概率密度函数在概念上不等,但在数值上相等。等式核心意思是:在给定一个θ和一个样本X时,整个事件发生的可能性多大。
四、极大似然估计的求解
假设总体分布族为{p(x;θ):θ ∈ 参数空间},其中p(x;θ)为概率分布列或密度函数为f(x;θ)。x1,x2,…,xn是简单样本,则样本的联合概率分布为:
① 离散型随机变量:
当样本x1,x2,…,xn给定时,p(x1,x2,…,xn;θ)是参数θ的函数,称这个函数为似然函数,记为L(θ;x1,x2,…,xn),或L(θ;x),或L(θ),即
具体求解步骤:
(1)构造似然函数 L(θ) :
总体X为离散型 ;
;
总体X为连续型:  ;
;
(2)取对数: lnL(θ) :
总体X为离散型: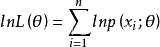 ;
;
总体X为连续型: 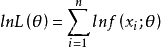 ;
;
(3)对Ln L(θ)求偏导等于0;
(4)解似然方程得到 θ 的极大似然估计值 θ^ 。
五、极大似然估计的优点与缺点
| 优点 | 缺点 |
|
①不变性 |
①前提是分布已知,要求较高 |
六、其他参数估计方法
矩估计:
以样本矩估计总体中相应的参数,以样本矩的函数估计总体矩的函数。
最小二乘估计(LSE):
通过最小化误差的平方和寻找数据的最佳函数匹配。具体为:找一个(组)估计值,使 得实际值与估计值之差的平方加总之后的值最小。这时,将这个差的平方的和式对参数求导 数,并取一阶导数为零,就是LSE。
贝叶斯估计:
贝叶斯估计是包含先验假设的极大似然估计,是对极大似然估计的一种改进。认为待估 参数θ也是随机的,我们可以根据先验信息建立一个θ服从的分布,合理利用先验信息进行统 计判断。
七、极大似然估计(MLE)与最大后验估计(MAP)
| MLE | MAP |
| 极大似然估计是频率学派常用参数估计方法,认为事件本身就具有客观的不确定性,直接为事件本身建模,也就是说事件在多次重复实验中趋于一个稳定的值p,那么这个值就是该事件的概率。 |
贝叶斯学派不去试图解释 事件本身的随机性,而是从观察者角度出发,认为不确定性来源于观察者的知识不完备,在这种情况下,通过已经观察到的信息来描述最有可能推导的过程。 |
|
模型参数是个定值 |
模型参数源于某种潜在分布 |
|
MLE是求参数θ的值,使得似然函数P(x|θ)最大。 |
MAP希望θ不仅使似然函数最大,同时也希望θ本身出现的先验概率也最大。 |
极大似然估计与最大后验概率估计的区别在于对先验信息的了解程度,如果忽略模型参 数本身的概率的分布,或者认为参数服从0-1均匀分布,那么最大后验概率估计将弱化为最大 似然估计。
八、关于极大似然估计的总结
极大似然估计是生产生活中一种常用的参数估计方法,它是根据已出现的样本结果,来推测导致该结果出现概率最大的模型参数θ。例如:在二分类机器学习模型logistic回归中,可以通过MLE估计模型参数,再使用其他方法进行参数优化。MLE是一种较为简单的估计,当样本数目增加时,收敛性很好,如果在假设的概率模型正确,通常能获得较好的结果。
参考
- https://zhuanlan.zhihu.com/p/428356533
- https://blog.csdn.net/weixin_43999327/article/details/99706044
- https://www.cnblogs.com/LittleHann/p/7823421.html#_lab2_3_0

