
总说
RNN( Recurrent Neural Network 循环(递归)神经网络) 跟人的大脑记忆差不多。我们的任何决定,想法都是根据我们之前已经学到的东西产生的。RNN通过反向传播和记忆机制,能够处理任意长度的序列,在架构上比前馈神经网络更符合生物神经网络的结构,它的产生也正是为了解决这类问题而应用而生的。
RNN及改进的LSTM等深度学习模型都是基于神经网络而发展的起来的认知计算模型。从原理来看,它们都是源于认知语言学中的“顺序像似性”原理:文字符号与其上下文构成一个“像”,这个“像”可以被认为是符号与符号的组合——词汇,也可以被认为是词汇与词汇的句法关系——依存关系。算法的训练过程,是通过正向和反馈两个过程从训练语料中学习出识别这些“像”的能力,并记录下“像”的模型数据,当输入的新的句子时,算法可以利用存储的模型数据识别出新输入中类似的“像”。
RNN的5种不同架构
one to one:
一个输入(单一标签)对应一个输出(单一标签)。
one to many:
一个输入对应多个输出,即这个架构多用于图片的对象识别,即输入一个图片,输出一个文本序列。
many to one:
多个输入对应一个输出,多用于文本分类或视频分类,即输入一段文本或视频片段,输出类别。
many to many 1:
这种结构广泛的用于机器翻译,输入一个文本,输出另一种语言的文本。
many to many 2:
这种广泛的用于序列标注。
在众多的深度学习网络中,RNN由于能够接收序列输入,也能得到序列输出,在自然语言处理中取得了巨大的成功,并得到广泛的应用。
Simple-RNN
先介绍RNN最简单的循环神经网络,称为Simple-RNN,它是后面LSTM的基础。从网络架构上,Simple-RNN与BP神经网络一脉相承,两个网络都有前馈层和反馈层,但Simple-RNN引入的基于时间的循环机制,因此而发展了BP网络。下面从整体上考察Simple-RNN的架构和训练运行。
Simple-RNN的神经网络
神经网络为A,通过读取某个t时间(状态)的输入x_t,然后输出一个值h_t。循环可以使得从当前时间步传递到下一个时间步。
这些循环使得RNN可以被看做同一个网络在不同时间步的多次循环,每个神经元会把更新的结果传递到下一个时间步,为了更清楚的说明,将这个循环展开,放大该神经网络A,看一下网络细节:
RNN神经元在不同步的传递
递归网络的输入是一整个序列,也就是x=[ x_0, … , x_t-1, x_t, x_t+1, x_T ],对于语言模型来说,每一个x_t将代表一个词向量,一整个序列就代表一句话。h_t代表时刻t的隐含状态,y_t代表时刻t的输出。
其中:
U:输入层到隐藏层直接的权重
W:隐藏层到隐藏层的权重
V: 隐藏层到输出层的权重
RNN展开以后,似乎都已经很明白了,正向传播( Forward Propagation ) 依次按照时间的顺序计算一次即可,反向传播( Back Propagation ) 从最后一个时间将累积的残差传递回来即可,跟普通的BP神经网络训练并没有本质上的不同。由于加入了时间顺序,计算的方式有所不同,这称为BPTT ( Back Propagation Through Time ) 算法。该算法的细节如下:
1.正向传播
首先在t=0的时刻,U、V、W都被随机初始化好了,h_0通常初始化为0,然后进行如下计算:
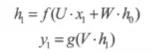
其中,f ,g 是激活函数,g通常是Softmax。
注:RNN有记忆能力,正是因为这个 W,记录了以往的输入状态,作为下次的输出。这个可以简单的理解为:
![]()
全局误差为:
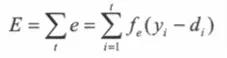
E是全局误差,e_i是第i个时间步的误差,y是输出层预测结果,d是实际结果。误差函数f_e可以为交叉熵( Cross Entropy ) ,也可以是平方误差项等。
2.反向传播
就是利用输出层的误差e( Cost Function ) ,求解各个权重derta_V、darta_U、derta_W,然后梯度下降更新各个权重。
各个权重的更新的递归公式:
现在的问题是如何求解各个权重的梯度,即:
求解的顺序分为如下两步,首先我们知道
![]()
对于任何代价函数,直接求取每一时刻的![]() 。得到derta_V,由于它不依赖之前的状态,可以直接求导获得。然后简单相加即可:
。得到derta_V,由于它不依赖之前的状态,可以直接求导获得。然后简单相加即可:![]()
但是derta_U、derta_W依赖于之前的状态,不能直接求导,需要定义中间变量:
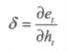
依次类推,知道输出层:
![]()
这里的*表示点乘。通过下面的计算出derta_U,derta_W:
到这里,Simple-RNN原理也就讲解完了。但是实际应用中并不多,因为:
a:如果出入越长的话,展开的网络就越深,对于“深度”网络训练的困难最常见的是“梯度爆炸( Gradient Explode )” 和 “梯度消失( Gradient Vanish )” 的问题。
b:Simple-RNN善于基于先前的词预测下一个词,但在一些更加复杂的场景中,例如,“我出生在法国……我能将一口流利的法语。” “法国”和“法语”则需要更长时间的预测,而随着上下文之间的间隔不断增大时,Simple-RNN会丧失学习到连接如此远的信息的能力。
LSTM原理
LSTM,即Long Short Term Memory Networks 长短时间记忆网络,是RNN的一个变种,专门用于解决Simple-RNN上述的俩问题。
LSTM通过对循环层的刻意设计来避免长期依赖和梯度消失,爆炸等问题。长期信息的记忆在LSTM中是默认行为,而无需付出代价就能获得此能力。
从网络主题上来看,RNN和LSTM是相似的,都具有一种循环神经网络的链式形式。在标准的RNN中,这个循环节点只有一个非常简单的结构,如一个tanh层。LSTM的内部要复杂得多,在循环的阶段内部拥有更多的复杂的结构,即4个不同的层来控制来控制信息的交互。
LSTM整体架构图与图例
一些必要的图例:
如下图,LSTM中在图上方贯穿运行的水平线指示了隐藏层中神经细胞cell的状态,类似于传送带,只与少量的线交互。数据直接在整个链上运行,信息在上面流动会很容易保持不变。状态C的变化受到控制门的影响。
LSTM有通过精心设计的称作“门”的结构来除去或者增加信息到细胞状态的能力。门是一种让信息选择式通过的方法。
下图就是一个门,包含一个Sigmoid网络层和一个Pointwise乘法操作。LSTM拥有三个门,来保护和控制细胞状态。0代表“不允许任何量通过”,1代表“允许任何量通过”。
控制门
逐渐理解LSTM
遗忘门
首先,决定从细胞状态中丢弃什么信息。这个决策是通过一个称为“遗忘门”的层来完成的。该门会读取 h_t-1 和 x_t,使用sigmoid函数输出一个在0-1之间的数值,输出给在状态C_t-1中每个细胞的数值。
输入和更新
然后确定什么样的新信息被存放在细胞状态中。这里包含两部分:
一部分是Sigmoid层,称为“输入门”,它决定我们将要更新什么值;
另一部分是tanh层,创建一个新的候选值向量~C_t,它会被加入到状态中。
这样,就能用这两个信息产生对状态的更新。
更新细胞状态
现在是更新旧细胞状态的时间了,C_t-1 更新为 C_t 。前面的步骤已经决定了将会做什么,现在就是实际去完成。把旧状态与 f_t 相乘,丢弃掉我们确定需要丢掉的信息,接着加上i_t*~C_t。这就是新的候选值,根据更新每个状态的程度进行变化。
在语言模型的例子中,这就是我们实际根据前面的目标,丢弃旧代词的类别信息并添加新的信息的地方。
输出信息
最终需要确定输出什么值。这个输出将会基于细胞状态,但也是一个过滤后的版本。首先,运行一个Sigmoid层来确定细胞状态的哪个部分将输出出去。接着,把细胞状态通过tanh进行处理( 得到一个在 -1~1 之间的值 ) 并将它和Sigmoid门相乘,最终仅仅会输出我们确定输出的那部分。
与RNN相同,都要最小化损失函数 l(t)。下面用 h(t) 表示当前时刻的隐藏层输出,y(t)表示当前时刻的输出标签,参考在后面的代码使用的是平方差损失函数,则损失函数被表示为:
![]()
全局化的损失函数如下:
通过梯度法,实现损失函数最小化参数估计。由于损失函数 l(t) 依赖于隐藏层 h(t) 和 输出层 y(t),根据链式法则,得到下式:
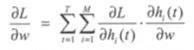
这里w是模型权重的标量,M是记忆单元的长度,i是隐藏层的第i个记忆单元,h_i(t)是一个标量,表示隐藏层第i个记忆单元的输出。由于网络随时间正向传播,改变h_i(t) 将不会影响到先于时间t的损失。
引入一个变量L(t),它表示了第i步开始到结束的损失。
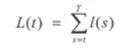
上述函数变更如下:
![]()
求解这个式子的最优化结果:
联立这个式子的最优化结果:
![]()
上式右侧的第一项来自简单的损失函数l(t)的时间t的导数。第二项的本质是一个循环项,它表明,计算当前节点的导数的信息时,需要下一节点的导数信息。这与RNN网络反向传播的过程相同,这里不再详细说明。
参考资料:
NLP自然语言处理原理与实践–书
RNN介绍,较易懂 –CSDN
cs22D_deeplearning for NLP — Stanford 视频
更多精彩内容,请关注 深度学习自然语言处理 公众号,就是下方啦!跟随小博主,每天进步一丢丢!哈哈!





















