循环神经网络

一.研究背景

• 1933年，西班牙神经生物学家Rafael Lorente de Nó发现大脑皮层（cerebral cortex）的解剖结构允许刺激在神经回路中循环传递，并由此提出反响回路假设（reverberating circuit hypothesis）
• 1982年，美国学者John Hopfield基于Little (1974) [12] 的神经数学模型使用二元节点建立了具有结合存储（content-addressable memory）能力的神经网络，即Hopfield神经网络
• 1986年，Michael I. Jordan基于Hopfield网络的结合存储概念，在分布式并行处理（parallel distributed processing）理论下建立了新的循环神经网络，即Jordan网络，也被称为简单循环网络
• 1989年，Ronald Williams和David Zipser提出了循环神经网络的实时循环学习（Real-Time Recurrent Learning, RTRL） [20] 。随后Paul Werbos在1990年提出了循环神经网络的随时间反向传播（BP Through Time，BPTT） [21] ，RTRL和BPTT被沿用至今，是循环神经网络进行学习的主要方法
• 1991年，Sepp Hochreiter发现了循环神经网络的长期依赖问题（long-term dependencies problem），即在对序列进行学习时，循环神经网络会出现梯度消失（gradient vanishing）和梯度爆炸（gradient explosion）现象，无法掌握长时间跨度的非线性关系，为解决长期依赖问题，大量优化理论得到引入并衍生出许多改进算法

二.简介

RNN的目的使用来处理序列数据。在传统的神经网络模型中，是从输入层到隐含层再到输出层，层与层之间是全连接的，每层之间的节点是无连接的。但是这种普通的神经网络对于很多问题却无能无力。例如，你要预测句子的下一个单词是什么，一般需要用到前面的单词，因为一个句子中前后单词并不是独立的。RNN之所以称为循环神经网路，即一个序列当前的输出与前面的输出也有关。具体的表现形式为网络会对前面的信息进行记忆并应用于当前输出的计算中，即隐藏层之间的节点不再无连接而是有连接的，并且隐藏层的输入不仅包括输入层的输出还包括上一时刻隐藏层的输出。理论上，RNN能够对任何长度的序列数据进行处理。但是在实践中，为了降低复杂性往往假设当前的状态只与前面的几个状态相关，下图便是一个典型的RNN：

（图片来自网络）

三. 结构

（图片来自网络）

3.1 循环结构

规范化一点, 正如上面的例子一样,当前的数据依赖于之前的信息, 设有一状态序列数据{st}

要表示这一性质,典型的处理方式:
st=f(st−1,θ)

其中f() 为映射(在RNN中可以简单的理解激活函数), θ 为参数. 从上式可以看出, 1). 映射是与时间不相关的. 2). θ 也是与时间无关的,这里体现了循环结构(在RNN中)的很重要性质: 参数(主要为权值参数)共享(parameter sharing).

上式可以用另一种形式(展开式)表示:

如果状态序列中的每个数据不只受其前面信息的影响,还受外部信息的影响,那么循环结构可以表示成:
st=f(st−1,xt,θ)

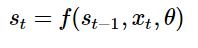
其中xt为外部信息序列的第t个元素. 这个就是RNN(简单的)使用的循环结构.

写成带权重的形式:
st=f(Wst−1+Uxt+bt)

为简洁,可以把偏置省略,可以将其看成是U中的(额外)第一维(元素都为 1),后面的BPTT推导将采用此种方式.

如果考虑输出层:

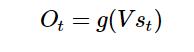
3.2 RNN 结构

3.3 双向循环神经网络结构

（图片来自网络）

前面介绍的循环神经网络是单向的，每一个时刻的输出依赖于比它早的时刻的输入值，这没有利用未来时刻的信息，对于有些问题，当前时刻的输出不仅与过去时刻的数据有关，还与将来时刻的数据有关，为此Schuster等人设计了双向循环神经网络[9]，它用两个不同的循环层分别从正向和反向对数据进行扫描。正向传播时的流程为：

1.循环，对t=1,…T

用正向循环层进行正向传播，记住每一个时刻的输出值

结束循环

2.循环，对t=T,…1

用反向循环层进行正向传播，记住每一个时刻的输出值

结束循环

3.循环，对所有的t，可以按照任意顺序进行计算

用正向和反向循环层的输出值作为输出层的输入，计算最终的输出值

结束循环

下面用一个简单的例子来说明，假设双向循环神经网络的输入序列为x1,…,x4。首先用第一个循环层进行正向迭代，得到隐含层的正向输出序列：

在这里由x1决定，由x1，x2决定，由x1 , . . . , x3决定，由x1 , . . . , x4 决定。即每个时刻的状态值由到当前时刻为止的所有输入值序列决定，这里利用的是序列的过去信息。然后用第二个循环层进行反向迭代，输入顺序是x4 , …, x1，得到隐含层的反向输出序列：

在这里，由x4决定，由x4, x3决定，由x4,…,x2 决定，由x4,…,x1决定。即每个时刻的状态值由它之后的输入序列决定，这里利用的是序列未来的信息。

然后将每个时刻的隐含层正向输出序列和反向输出序列合并起来：

送入神经网络中后面的层进行处理，此时，各个时刻的处理顺序是随意的，可以不用按照输入序列的时间顺序。

3.4 深度循环神经网络

（图片来自网络）

上面我们介绍的循环神经网络只有一个输入层，一个循环层和一个输出层，这是一个浅层网络。和全连接网络以及卷积网络一样，我们可以把它推广到任意多个隐含层的情况，得到深度循环神经网络[11]。

这里有3种方案，第一种方案为Deep Input-to-Hidden Function，在循环层之前加入多个普通的前馈层，将输入向量进行多层映射之后再送入循环层进行处理。

第二种方案是Deep Hidden -to-Hidden Transition，它使用多个循环层，这和前馈型神经网络类似，唯一不同的是计算隐含层输出的时候需要利用本隐含层在上一个时刻的输出值。

第三种方案是Deep Hidden-to-Output Function，它在循环层到输出层之间加入多前馈层，这和第一种情况类似。

由于循环层一般用tanh作为激活函数，层次过多之后会导致梯度消失问题，和残差网络类似，可以采用跨层连接的方案。在语音识别、自然语言处理问题上，我们会看到深层循环神经网络的应用，实验结果证明深层网络比浅层网络有更好的精度。

四. 训练算法—–BPTT算法

前面我们介绍了循环神经网络的结构，接下来要解决的问题是网络的参数如何通过训练确定。由于循环神经网络的输入是时间序列，因此每个训练样本是一个时间序列，包含多个相同维度的向量。解决循环神经网络训练问题的算法是Back Propagation Through Time算法，简称BPTT[2-4]，原理和标准的反向传播算法类似，都是建立误差项的递推公式，根据误差项计算出损失函数对权重矩阵、偏置向量的梯度值。不同的是，全连接神经网络中递推是在层之间建立的，而这里是沿着时间轴建立的。

BPTT算法伪代码

五.循环神经网络面临的挑战

循环神经网络与其他类型的神经网络共同要面对的是梯度消失问题，对此出现了一些解决方案，如LSTM等。相比卷积神经网络，循环神经网络在结构上的改进相对要少一些。

5.1梯度消失问题

和前馈型神经网络一样，循环神经网络在进行梯度反向传播时也面临着梯度消失和梯度爆炸问题，只不过这种消逝问题表现在时间轴上，即如果输入序列的长度很长，我们很难进行有效的梯度更新。

梯度消失问题发生时，靠近输出层的hidden layer 3的权值更新相对正常，但是靠近输入层的hidden layer1的权值更新会变得很慢，导致靠近输入层的隐藏层权值几乎不变，扔接近于初始化的权值。这就导致hidden layer 1 相当于只是一个映射层，对所有的输入做了一个函数映射，这时此深度神经网络的学习就等价于只有后几层的隐藏层网络在学习。

5.2 如何解决梯度消失？

梯度消失和梯度爆炸问题都是因为网络太深，网络权值更新不稳定造成的，本质上是因为梯度反向传播中的连乘效应。对于更普遍的梯度消失问题，可以考虑以下三种方案解决：

• 用ReLU、Leaky ReLU、PReLU、RReLU、Maxout等替代sigmoid函数。
• 用Batch Normalization。
• LSTM的结构设计也可以改善RNN中的梯度消失问题。

参考：
《深度学习》 花书
复旦大学 《深度学习》