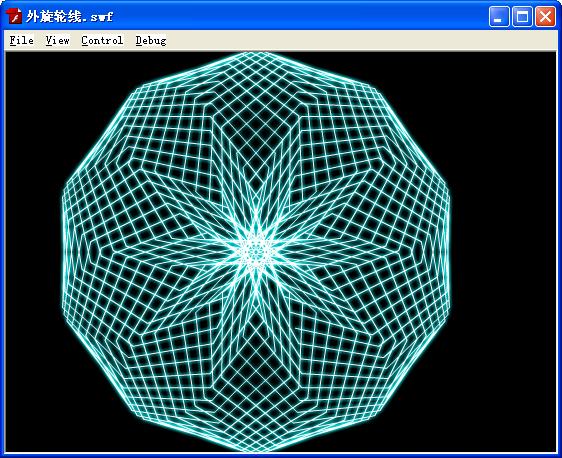
旋轮线又称为摆线,它所滚动的轨迹可能是一直线或者圆,不同的情况下产生的轨迹曲线会有所不同。其中一种是内摆线,一种是外摆线。这种线的描述可以在高等数学几何里面找到,或者百度搜索当中可以搜索到相关的资料。在写这部分内容的时候,其实很多的时候借用数学公式产生的图案结合到编程当中,一方面加深编程,一方面了解解析几何对flash编程的作用。它所的作用会给我们带了很多意想不到灵感,知道之后,你会利用到这部分知识结合到实现当中。
今晚,一边听着二胡的歌曲,一边书写一下博客。有时候,写技术的文章会比较鼓噪一点,不过当你热爱了写作之后。这种习惯就很难去改掉。个人有一种习惯就是懒得去改变,当熟悉之后就会显得对他产生一种爱慕的感情。也许这就是一种喜欢。
在一些数学网站里面,找了外摆线的资料。它的参数方程如下:a和b 为半径,θ 为角度。
x=(a+b)cosθ-bcos[(a+b)θ/b]; y=(a+b)sinθ-bsin[(a+b)θ/b];
通常,会利用这种参数方程的描绘这种曲线的形状。我所在思路都是采用360的循环描绘线。
初始的时候,我们需要定义画笔,定义半径和开始位置点。这样就可以为后面封装带来帮助。
默认的flash文档一般为550×400。

package { //创建外旋轮线 // x=(a+b)cosθ-bcos[(a+b)θ/b]; y=(a+b)sinθ-bsin[(a+b)θ/b]; import flash.display.Sprite; import flash.events.*; import flash.display.Shape; public class Main2 extends Sprite { private var pen:Shape=new Shape();//创建画笔用于绘图 private var startX:Number=250;//绘制图形的开始点x坐标 private var startY:Number=200;//绘制图形开始点的y坐标 private var a_radius:Number=100;//大圆半径 private var b_raidius:Number=10;//小圆半径 public function Main2() { CreatCycloid(); } //创建外旋轮线 private function CreatCycloid():void { pen.graphics.lineStyle(1); addChild(pen); for (var i:int=0; i<360; i++) { var rad:Number=i*Math.PI/180; var x1:Number=startX+(a_radius+b_raidius)*Math.cos(rad)-b_raidius*Math.cos((a_radius+b_raidius)*rad/b_raidius); var y1:Number=startY+(a_radius+b_raidius)*Math.sin(rad)-b_raidius*Math.sin((a_radius+b_raidius)*rad/b_raidius); if (i==0) { pen.graphics.moveTo(x1,y1); } pen.graphics.lineTo(x1,y1); } } } }
创建完毕之后,我们对这种线加一个圆看看效果图会发生什么事情。它看起来会像一条花朵。

private function CreatCycloid():void { pen.graphics.lineStyle(1); addChild(pen); pen.graphics.beginFill(0x00ff00); for (var i:int=0; i<360; i++) { var rad:Number=i*Math.PI/180; var x1:Number=startX+(a_radius+b_raidius)*Math.cos(rad)-b_raidius*Math.cos((a_radius+b_raidius)*rad/b_raidius); var y1:Number=startY+(a_radius+b_raidius)*Math.sin(rad)-b_raidius*Math.sin((a_radius+b_raidius)*rad/b_raidius); if (i==0) { pen.graphics.moveTo(x1,y1); } pen.graphics.lineTo(x1,y1); } pen.graphics.drawCircle(startX,startY,a_radius); }
再接下来,加以填充底色看看效果又如何?这两个图案交集下产生了什么影响?

private function CreatCycloid():void { pen.graphics.lineStyle(1); addChild(pen); pen.graphics.beginFill(0x00ff00); for (var i:int=0; i<360; i++) { var rad:Number=i*Math.PI/180; var x1:Number=startX+(a_radius+b_raidius)*Math.cos(rad)-b_raidius*Math.cos((a_radius+b_raidius)*rad/b_raidius); var y1:Number=startY+(a_radius+b_raidius)*Math.sin(rad)-b_raidius*Math.sin((a_radius+b_raidius)*rad/b_raidius); if (i==0) { pen.graphics.moveTo(x1,y1); } pen.graphics.lineTo(x1,y1); } pen.graphics.drawCircle(startX,startY,a_radius); pen.graphics.endFill(); }
交集下产生这种像花朵一样的图案了。
如果觉得没意思,那么我们可以借助一些图案组合,变化出什么得意的创作,
太极花朵。

我们恰当修改了这条方程式的一些值就会变成另外一种很有趣的图案了。
至于是如何? 留一个悬念在这里!