复变函数：傅里叶级数

1 对周期函数进行分解的猜想

拉格朗日等数学家发现某些周期函数可以由三角函数的和来表示，比如下图：

而后，其他数学家猜测任意周期函数都可以写成三角函数之和。

2 分解的思路

常数项的分解

根据周期函数的定义，常数函数是周期函数，其周期是任意实数，所以，对于 $y=C,C∈Ry=C,C\in \mathbb{R}$ 这样的常数函数，分解里面要添加一个常数项与之对应。

其他部分的分解

其他部分可以通过 $sin⁡(x),cos⁡(x)\sin(x),\cos(x)$ 两个三角进行分解，主要思路如下：

$sin⁡(x),cos⁡(x)\sin(x),\cos(x)$ 是周期函数，进行合理的加减组合，结果可以是周期函数，且它们的微分和积分都很简单。
任意函数都可以分解成奇偶函数之和：
$f(x)=f(x)+f(−x)2+f(x)−f(−x)2=feven+foddf(x)={f(x)+f(-x)\over 2}+{f(x)-f(-x)\over 2}=f_{even}+f_{odd}$
$sin⁡(x)\sin(x)$ 是奇函数，奇函数与奇函数加减永远是奇函数
$cos⁡(x)\cos(x)$ 是偶函数，偶函数和偶函数加减永远是偶函数

保证组合的周期为T

之前提到 $f (x)$ 是周期为T的函数，那么怎么保证组合出来的函数周期仍然为T呢？

首先，我们知道 $sin⁡(x)\sin(x)$ 的周期为 $2π2\pi$ ， $sin⁡(2x)\sin(2x)$ 的周期也是 $2π2\pi$ ，但是最小周期是 $π\pi$ ，很显然， $sin(nx),n∈Nsin(nx),n\in N$ 的周期都是 $2π2\pi$ 。所以更一般地，如果 $f (x)$ 的周期为T，那么 $sin(2πnTx),cos(2πnTx),n∈Nsin({2\pi n\over T}x),cos({2\pi n\over T}x),n\in N$ 这些函数的周期也为T，将这些函数进行加减，就保证了得到的函数周期也为T。

调整振幅

假如有如下这个函数，周期为 $2π2\pi$ ：

现在我们也有一些周期为 $2π2\pi$ 的函数，比如 $s i n (x), s i n (2 x), s i n (3 x), s i n (4 x), s i n (5 x)$ ：

通过调整振幅可以让它们慢慢接近目标函数，比如 $s i n (x)$ 处处小于目标函数：

将其振幅增大一倍可得 $2sin⁡(x)2\sin(x)$ ：

此时 $2 s i n (x)$ 有地方超出目标函数，此时我们从周期为 $2π2\pi$ 的函数中选择一个，减去一点（下面以 $2 s i n (x) - s i n (2 x)$ 为例）：

通过调整振幅，加加减减，我们可以慢慢接近目标函数：

综上，构造出来的三角函数和类似于如下的样子：

复变函数：傅里叶级数-编程之家
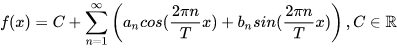
这符合之前的分析：

有常数项
用奇函数和偶函数组合出任意函数
周期为T
调整振幅，逼近原函数

3 $sin⁡(x),cos⁡(x)\sin(x),\ \cos(x)$ 的另外一种表示方法

欧拉公式：

$eiθe^{i\theta}$ 代表复平面一个夹角为 $θ\theta$ 的向量：

当 $θ\theta$ 不再是常数，而是代表时间的变量t的时候： $eiθ→eite^{i\theta }\to e^{it}$ ，随着时间t的增长， $θ\theta$ 不断增大，这个向量就会旋转起来， $2π2\pi$ 的时间会旋转一圈，这就是 $T=2πT=2\pi$

通过欧拉公式表示 $s i n (t)$

根据欧拉公式，有： $e^{it}=cos(t)+isin(t)$ ，所以，在时间轴t上，把 $e^{it}$ 向量的虚部（也就是纵坐标）记录下来，得到的就是 $s i n (t)$ ：

代数上用 $I m$ 表示虚部：

$sin(t)=Im(e^{it})$

作为对比，记录 $e^{i2t}$ 的虚部，此时我们可以得到 $s i n (2 t)$ ：

如果在时间轴t上，把 $e^{it}$ 的实部（横坐标）记录下来，得到的就是 $c o s (t)$ 的曲线：

代数上使用 $R e$ 代表实部：

$cos(t)=Re(e^{it})$

更一般的，在 $e^{iwt}$ 图像中，我们可以观察到旋转的频率（能反应不同频率旋转的快慢，下面的动图更好理解），所以称为频域；而在 $sin⁡(t)\sin (t)$ 图像中我们可以观察到流逝的时间，所以称为时域：

4 通过频域求系数：

假设有这么一个函数：

$g (x) = s i n (x) + s i n (2 x)$

可以看出这是一个 $T=2πT=2\pi$ 的函数：

如果转到频域去，那么函数 $g (x)$ 就是下面这个复数函数的虚部：

$g(t)=Im(e^{it}+e^{2it})$

我们先看下 $eiθ+ei2θe^{i\theta}+e^{i2\theta}$ ，其中 $θ\theta$ 是常数，很显然这是两个向量之和：

将 $θ\theta$ 换成流逝的时间t，并将虚部记录下来，此时就得到了 $g (t)$ ：

函数向量

从上面的讨论我们可以看出， $e^{iwt}$ 是一个旋转的向量。而根据欧拉公式，有：

$e^{iwt}=cos(wt)+isin(wt)$

从图像上看：

这里 $s i n (w t), c o s (w t)$ 也是向量。

$e^{iwt},sin(wt),cos(wt)$ 都称为函数向量，其点积定义如下：

待补充

g(t)是一个线性组合

从上面的讨论，我们可以得到 $s i n (t), s i n (2 t)$ 是函数向量，那么它们的线性组合得到的也是函数向量：

$g (t) = s i n (t) + s i n (2 t)$

根据点积定义有：

$sin(t)⋅sin(2t)=∫02πsin(t)sin(2t)dt=0sin(t)\cdot sin(2t)=\int_{0}^{2\pi}sin(t)sin(2t)dt=0$

根据点积的代数和几何意义（待补充）， $sin(t)⋅sin(2t)=0sin(t)\cdot sin(2t)=0$ 说明了这两个函数向量正交、线性无关且是正交基。

如果写成如下形式：

$g (t) = 1 s i n (t) + 1 s i n (2 t)$

那么就可以理解为 $g (t)$ 在正交基 $s i n (t), s i n (2 t)$ 下的坐标为 $(1, 1)$ 。

如何求正交基的坐标

假设

$w→=2u→+3v→\overrightarrow{w}=2\overrightarrow{u}+3\overrightarrow{v}$

其中， $u→=(11),v→=(−11)\overrightarrow{u}=\begin{pmatrix}1\\1\end{pmatrix},\overrightarrow{v}=\begin{pmatrix}-1\\1\end{pmatrix}$

通过点积：

$u→⋅v→=0\overrightarrow{u}\cdot\overrightarrow{v}=0$

可知这两个向量正交，是正交基， $w→\overrightarrow{w}$ 在基 $u→,v→\overrightarrow{u},\overrightarrow{v}$ 下的坐标为 $(2, 3)$ ，其中在基 $u→\overrightarrow{u}$ 下的坐标可以通过这种点积操作来计算（注意只有对正交基才能这么做）：

$w→⋅u→u→⋅u→=(−1,5)⋅(1,1)(−1,1)⋅(−1,1)=2{\overrightarrow{w}\cdot\overrightarrow{u}\over\overrightarrow{u}\cdot\overrightarrow{u}}={(-1,5)\cdot(1,1)\over(-1,1)\cdot(-1,1)}=2$

如何求 $sin⁡(nt)\sin(nt)$ 基下的坐标

对于

$g (x) = s i n (x) + s i n (2 x)$

其中 $g (x)$ 是向量， $s i n (t), s i n (2 t)$ 是正交基，周期 $T=2πT=2\pi$ 。

因为是正交基，根据刚才的分析，我们可以通过如下的方式求基 $s i n (t)$ 下的坐标：

$g(t)⋅sin(t)sin(t)⋅sin(t)=∫02πg(x)sin(x)dx∫02πsin2(x)dx=1\frac{g(t)\cdot sin(t)}{sin(t)\cdot sin(t)}=\frac{\int_0^{2\pi}g(x)sin(x)dx}{\int_0^{2\pi}sin^2(x)dx}=1$

更一般的情况

对于之前的假设，其中 $f (x)$ 的周期为T：
复变函数：傅里叶级数-编程之家
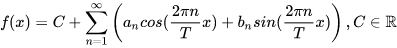
可以改写成这样：

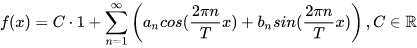
也就是说向量 $f (x)$ 是以下正交基的线性组合：

这里 $1$ 也是一个基，那么可以得到：

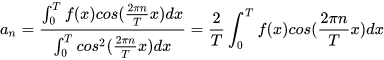
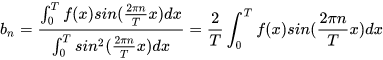
C也可以通过点积来表示，最终可以得到傅里叶级数的表达式：

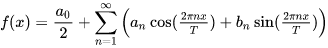
其中（下面的式子其实就是在求坐标）：