
Question A: The Force Overturning Of The Iron Pan.
典型的物理题,解题涉及到弹簧和力学知识,题目不多,涉及的物理知识也并不繁琐。想要答得出彩并不容易。
问题重述:
均质半球形薄铁锅,质量10kg,铁锅直径0.6m。罐直径两端有两个环(A、B),环的直径可以忽略不计。在环上安装相同的轻质弹簧等长硬弹簧,两个弹簧的端部也有环,两个环位于光滑杆上。环可以移动。弹簧不受力时,长度为0.8m,弹簧的顽固系数为750N/m。假设弹簧只能膨胀,不能弯曲。
问题1:假设弹簧总是直立的,试着回答以下问题:
(1) 如果在点a处施加90N的向下拉力,求出铁盘平衡状态下盘平面与水平面之间的角度。
(2) 如果以0.1s的间隔去除A点上施加的拉力,则给出10s内平面与水平面之间角度的变化数据。
(3) 找出两个弹簧的弹性势能在10秒内随时间变化的模型。
图1:问题1中模型的示意图
问题2:现在考虑一种情况,即现在有三个弹簧,环A、B和C位于三等分圆的三个点上,弹簧的参数保持不变,但此时三个弹簧的端部连接并悬挂在一个固定装置上。铁盘在支点上处于平衡状态,处于初始状态。尝试回答以下问题:
(1) 如果在点a所在直径另一端的点D处向下施加90N的拉力,则在铁罐平衡后,拉力被去除。每隔0.1s,锅平面与水平平面之间的角度变化以10s为单位。
图2:问题2的模型
涉及物理力学知识点:
胡克定律:F=kΔx。
弹性势能公式为:EP=1/2 k(Δx)^2。
弹性势能(Elastic Potential Energy)是物体因为弹性形变而具有的能量。
其中,k为弹性系数,Δx为压缩量。注意:此公式中的x必须在弹簧的弹性限度内。
物理加速度五大公式是a=mv^2/r、a=F/m、Vt^2-Vo^2=2as、Vt=Vo+at、a=(Vt-Vo)/t,加速度(Acceleration)是速度变化量与发生这一变化所用时间的比值Δv/Δt,是描述物体速度变化快慢的物理量,通常用a表示,单位是m/s。
物理学中用速度来表示物体运动的快慢和方向。速度在数值上等于物体运动的位移跟发生这段位移所用的时间的比值。速度的计算公式为v=Δs/Δt。
局部和整体平衡受力分析。
解题思路分析:
问题1-F=90N时倾斜角度
首先我们需要分析一下已知条件和未施加F时的平衡受力状态。
已知:均质铁锅的D=0.6m,(R=0.3m),10kg
弹簧的原长l=0.8m,k=750N/m(注意这里的原长不是挂着铁锅的,就是指弹簧的自然不受力状态下的长度)
列出如下假设:
假设1:弹簧只能膨胀,不能弯曲;
假设2:弹簧、圆环的自重均不考虑;
假设3:在施加外力与撤掉外力的过程中弹簧均在弹性范围内;
假设4:重力加速度g取9.8m/s²。
挂着铁锅的平衡状态分析(无其他外力)。
初始平衡状态整体受力分析
根据受力分析可列出如下方程:2k△x=10g
求得△x=0.0653m
则初始状态弹簧长度为l+△x=0.8653m
接着,施加F=90N后,根据常识,铁锅必然会倾斜,如图所示:
施加F外力后的整体受力分析
此时,弹簧连接的圆环也会随之向内滑动,锅的平面会与水平面形成一个夹角θ。
同时,锅的重心也会偏移,设偏移量为n,即n=Rsinθ。
对整体进行受力分析,得到方程:
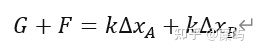
由几何关系可以得到方程:
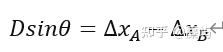
接着对锅的A、B两端进行局部受力分析。
局部受力分析
由此得到方程组:
下面我们讨论质心偏移量m对A、B两端承担G的影响:
其中,GA和GB的分配关系可以类比杠杆定理,即:
由此,我们获得了关于θ的方程组:
代入已知数据整理得到:
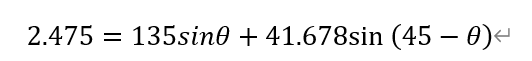
利用matlab求解方程功能即可求得答案:
问题1-撤去F=90N时10s内角度
此时需要考虑撤去F瞬间受力情况:
撤去F瞬间
列出弹簧收缩的加速度公式:F'+k△xA=ma
由于题目并未告知弹簧质量,结合假设,我们认为弹簧轻质可忽略重量m。由此只需分析物体的移动情况,这里需要考虑A/B两端。
分析过程和所需知识与前述相同,不过该问需要求出每间隔0.1s的角度数据,故方程组是和t有关的。
问题1-弹簧弹性势能
结合前面的分析,代入弹性势能公式EP=1/2 k(Δx)^2即可
弹性势能(Elastic Potential Energy)是物体因为弹性形变而具有的能量。
问题2-三根弹簧
属于问题1的外延,分析方法大同小异。
完整思路及第一问答案见评论区
欢迎交流评论~











